Use the information below to answer the following question. What is the pH of a 0.100 M solution of benzoic acid?
Use the information below to answer the following question. What is
the pH of a 0.100 M solution of benzoic acid?
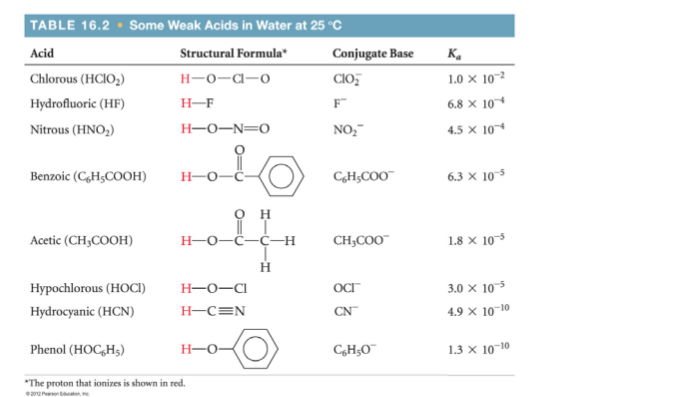
Use the information below to answer the following question. What is
the pH of a 0.100 M solution of benzoic acid?

1 Answer
Explanation:
Benzoic acid is a weak acid, whose dissociation we represent as:
Using the usual conventions,
Where
We have a quadratic in
I am not going to bother to do another approx. but perhaps you should; i.e. plug your first approx. back into the equation to see how the answer evolves.
And

