Question

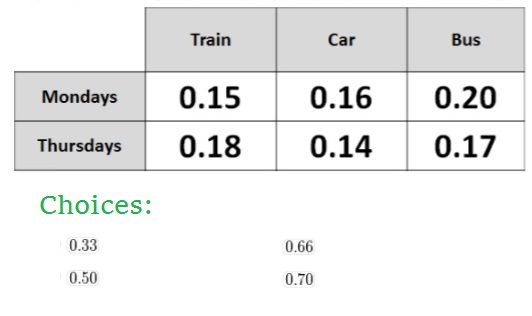
Use the table to calculate the probability that it is a Thursday, given that Jemma has travelled to work either by a train or a bus? The table show the relative frequencies with which Jemma uses each type of transport on her two travel day.

Answer 1

`P("Thursday"|"Train or bus")=0.5`

Explanation:

The probability is written as `P("Thursday"|"Train or bus")`, or "The probability it is a Thursday, given a train or bus was taken".

To fond this probability, we find the probability that either a bus or train was taken and divide it by the probability a bus or train was taken.

`P("Thursday"|"Train or bus")=(P("Train or bus on Thursday"))/(P("Train or bus was taken"))`

`P("Train or bus on Thursday")=0.18+0.17=0.35`

`P("Train or bus was taken")=0.18+0.17+0.15+0.20=0.70`

`P("Thursday"|"Train or bus")=0.35/0.70=1/2=0.5`

Answer 2

`0.50`

Explanation:

Note that `"Train"` / `"Car"` / `"Bus"` are mutually exclusive, as are `"Monday"` / `"Thursday"`.

For brevity, let us write:

`{ (T = "Train"), (C = "Car"), (B = "Bus"), ("Mo" = "Monday"), ("Th" = "Thursday") :}`

Then:

`P("Th" | (T uu B)) = (P("Th" nn (T uu B)))/(P(T uu B))`

Now:

`P("Th" nn (T uu B)) = P("Th" nn T) + P("Th" nn B) = 0.18 + 0.17 = 0.35`

and:

`P(T uu B) = P(("Mo" uu "Th") nn (T uu B))`

`color(white)(P(T uu B)) = P(("Mo" nn T) uu ("Mo" nn B) uu ("Th" nn T) uu ("Th" nn B))`

`color(white)(P(T uu B)) = P("Mo" nn T) + P("Mo" nn B) + P("Th" nn T) + P("Th" nn B)`

`color(white)(P(T uu B)) = 0.15+0.20+0.18+0.17 = 0.70`

So:

`P("Th" | (T uu B)) = (P("Th" nn (T uu B)))/(P(T uu B)) = 0.35/0.70 = 0.50`