Using the second derivative f''(x) = 36x^2-12, how do you find the intervals in which f is concave up and the intervals in which f is concave down?
2 Answers
Unlike the first derivative test where it explains how a function is increasing or decreasing, we are now determining the concavity of a function, or how a line curves up or down. By taking the second derivative and setting up an interval. we can answer where the function
Given
graph{x^3 [-5, 5, -5, 5]}
Notice that the concavity goes from down to up starting at the origin. This means that for
So, we can say that
Now, we should test some values around the inflection points to see if
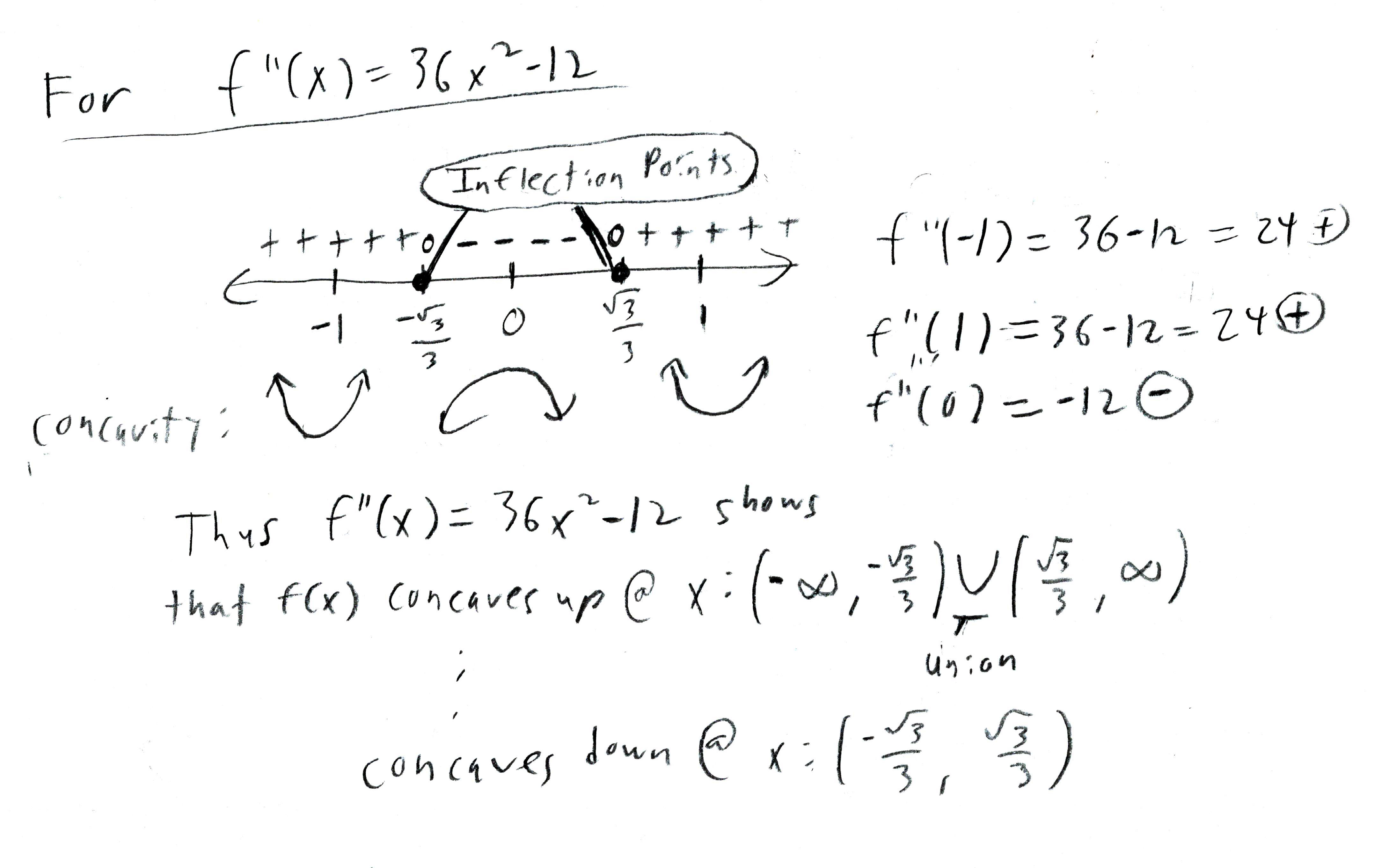
For
For
For
Note that a line cannot curve on the inflection points. The parentheses () indicate the greater than (
Here is a number line representation of the answer:
We are given:
Use your method of choice for solving the inequalities:
I like finding partition number (zeros) and testing the resulting intervals.
For his problem:
On
On
On
Alternative for this
The graph of


