Question

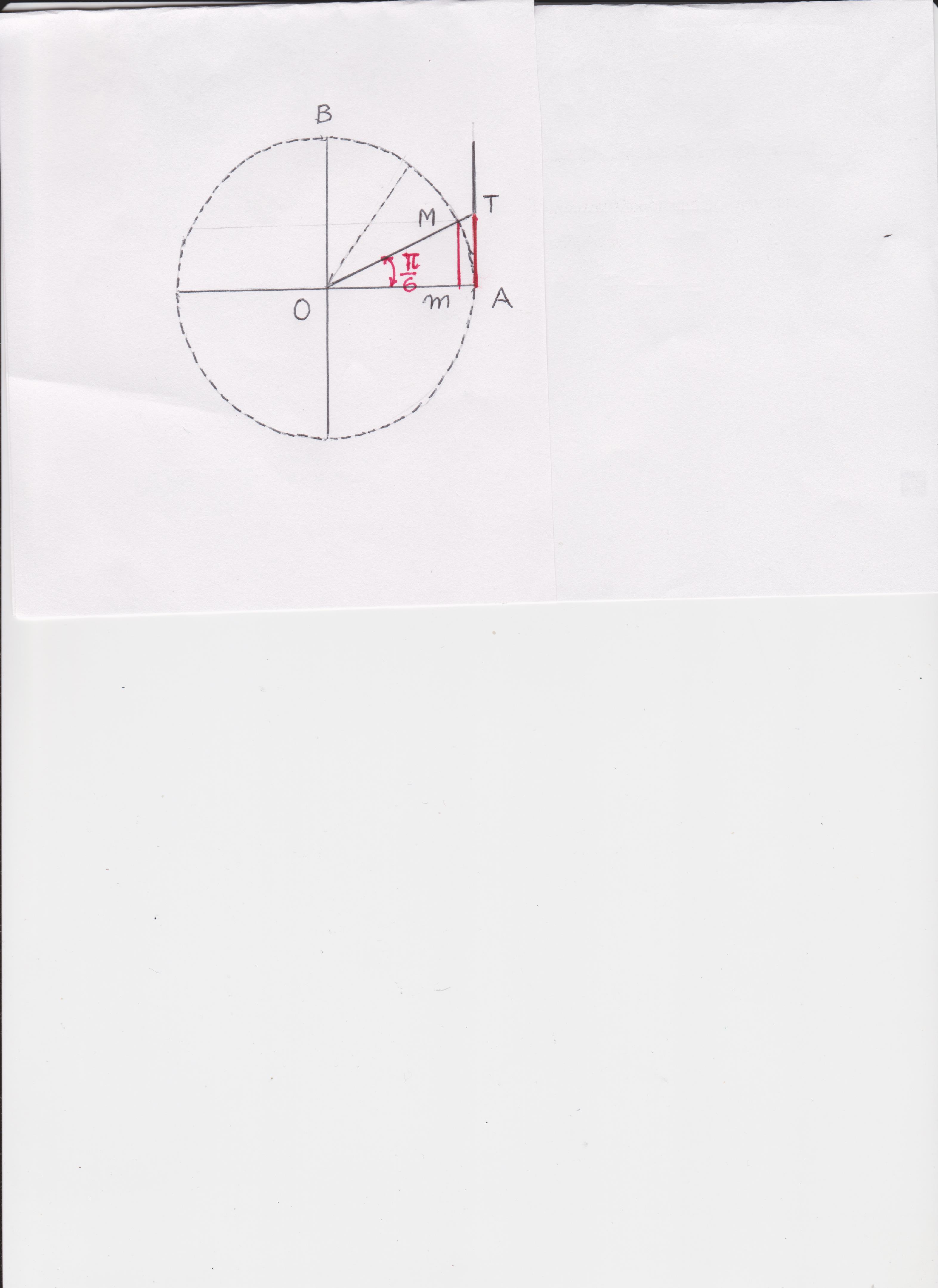
Using the unit circle, how do you find the value of the trig function: tan pi/6?

Answer 1

Find tan (pi/6) on the trig unit circle

Ans: `(sqrt3)/3`

Explanation:

On the trig unit circle, M being the terminal point of the arc `(pi/6)`
`AT = tan (pi/6)` (by definition)
OM = OA = R = 1 (definition of trig unit circle)
`Mm = (OM)/2 = 1/2` (equilateral triangle)
`Om = sqrt3/2` (height of equilateral triangle)

Triangle OAT and triangle OMm
`(AT)/(Mm) = (OA)/(Om)`--> `AT = (Mm)((OA)/(Om))`
`tan (pi/6) = (1/2)(1/(sqrt3/2)) = (1/2)(2/sqrt3) = 1/(sqrt3) = (sqrt3)/3`