Question

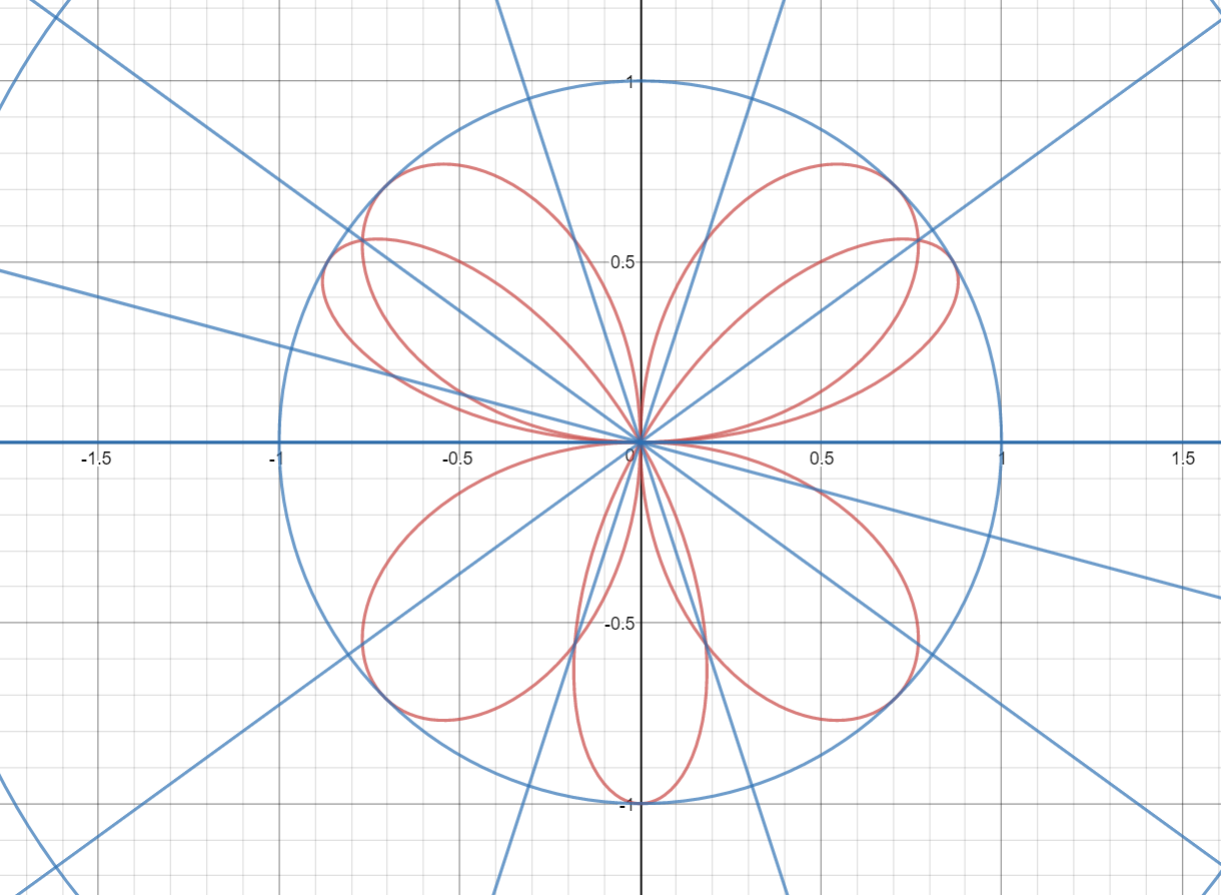
What are all the intersections of the graphs r=sin2theta and r=sin3theta?

What are all of the intersections of the graphs `r=sin2theta and r=sin3theta` ?

Answer 1

Solution for `theta` are given by `theta=(2n+1)pi/5` or `theta=2npi`, where `n` is an integer. Polar coordinates of solution are `{(0,0),(0.951,pi/5),(-0.588,(3pi)/5),(0,pi),(0.588,(7pi)/5),),(-0.951,(9pi)/5),(0,2pi)}`

Explanation:

Intersection of graphs of `r=sin2theta` and `r=sin3theta` will be there where

`sin2theta=sin3theta`

or `sin3theta-sin2theta=0`

or `2cos((3theta+2theta)/2)sin((3theta-2theta)/2)=0`

or `2cos((5theta)/2)sin(theta/2)=0`

i.e. either `(5theta)/2=(2n+1)pi/2` i.e. `theta=(2n+1)pi/5`

or `theta/2=npi` i.e. `theta=2npi`, where `n` is an integer.

In the interval `[0^@,360^@]`, solutions are `{0^@,36^@,108^@,180^@,252^@,324^@,360^@}`. In radians they are `{0,pi/5,(3pi)/5,pi,(7pi)/5,(9pi)/5,2pi}`

and putting this in `r=sin2theta` or `r=sin3theta`, corresponding values of `r` are `[0,0.951,-0.588,0,0.588,-0.951,0}`

and polar coordinates of solution are `{(0,0),(0.951,pi/5),(-0.588,(3pi)/5),(0,pi),(0.588,(7pi)/5),),(-0.951,(9pi)/5),(0,2pi)}`