Question

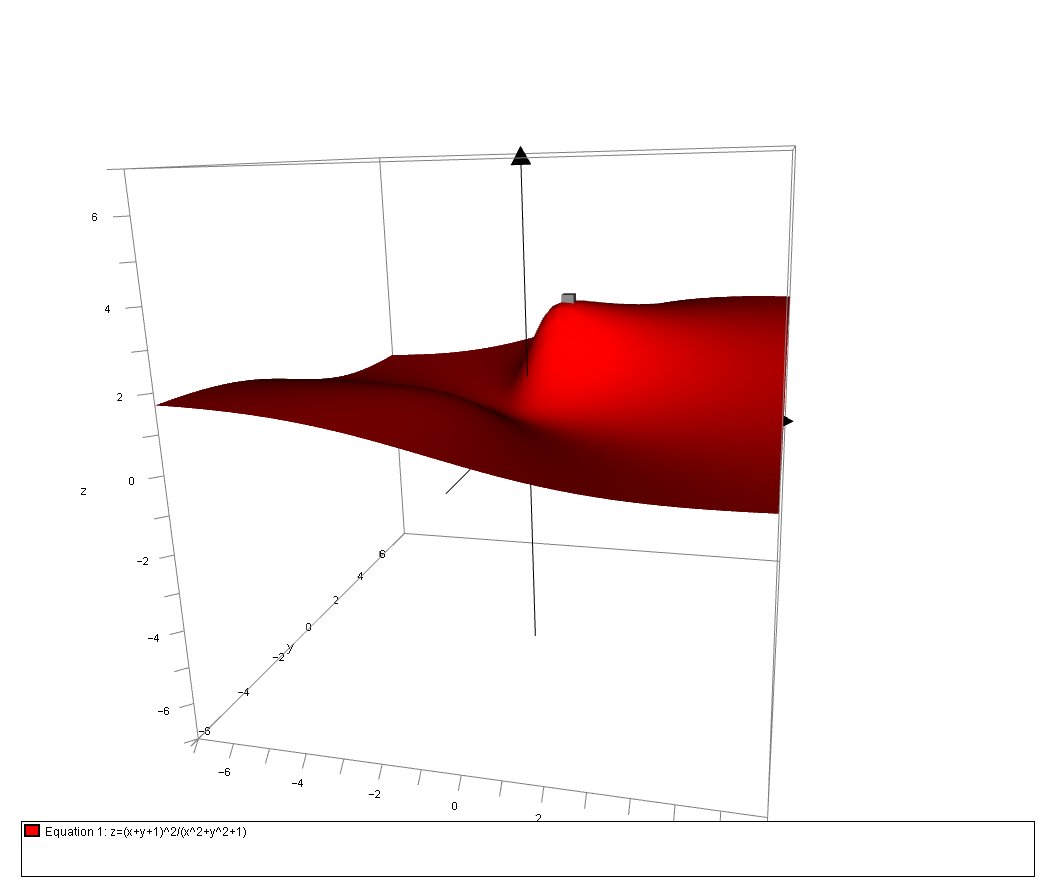
What are extrema and saddle points of `f(x,y)=(x+y+1)^2/(x^2+y^2+1)`?

Answer 1

Explanation:

We have:

`f(x,y) = (x+y+1)^2/(x^2+y^2+1)`

Step 1 - Find the Partial Derivatives

We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constant. Thus:

The First Derivatives are:

`f_x = { (x^2+y^2+1)(2(x+y+1)) - ((x+y+1)^2)(2x) } / (x^2+y^2+1)^2`
`\ \ \ = { 2(x^2+y^2+1)(x+y+1) - 2x(x+y+1)^2 } / (x^2+y^2+1)^2`
`\ \ \ = { 2(x+y+1)(x^2+y^2+1- x^2-xy-x) } / (x^2+y^2+1)^2`
`\ \ \ = { 2(x+y+1)(y^2-xy-x+1) } / (x^2+y^2+1)^2`

`f_y = { (x^2+y^2+1)(2(x+y+1)) - ((x+y+1)^2)(2y) } / (x^2+y^2+1)^2`
`\ \ \ = { 2(x^2+y^2+1)(x+y+1) - 2y(x+y+1)^2 } / (x^2+y^2+1)^2`
`\ \ \ = { 2(x+y+1)(x^2+y^2+1- y^2-xy-y) } / (x^2+y^2+1)^2`
`\ \ \ = { 2(x+y+1)(x^2-xy-y+1) } / (x^2+y^2+1)^2`

The Second Derivatives (quoted) are:

`f_(x x) = ( -4(-x^3-x^3y-3x^2y+3xy^2+3x+3xy^3+3xy+y^3+y ) ) / (x^2+y^2+1)^3`

`f_(yy) = (-4(3x^3y+x^3+3x^2y+3xy+x-xy^3-3xy^2+3y-y^3)) / (x^2+y^2+1)^3`

The Second Partial Cross-Derivatives are:

`f_(xy) = {2(-x^4-2x^3+6x^2y^2+6x^2y+6xy^2-2x+1-y^4-2y^3-2y)} / (x^2+y^2+1)^3`

`f_(yx) = {2(-x^4-2x^3+6x^2y^2+6x^2y+6xy^2-2x+1-y^4-2y^3-2y)} / (x^2+y^2+1)^3`

Note that the second partial cross derivatives are identical due to the continuity of `f(x,y)`.

Step 2 - Identify Critical Points

A critical point occurs at a simultaneous solution of

`f_x = f_y = 0 iff (partial f) / (partial x) = (partial f) / (partial y) = 0`

i.e, when:

`f_x = { 2(x+y+1)(y^2-xy-x+1) } / (x^2+y^2+1)^2 = 0`
`\ \ \ => (x+y+1)(y^2-xy-x+1) = 0` ..... [A]

`f_y = { 2(x+y+1)(x^2-xy-y+1) } / (x^2+y^2+1)^2 = 0`
`\ \ \ => (x+y+1)(x^2-xy-y+1) = 0` ..... [B]

Solving [A] and [B] simultaneously, we gain a single solution:

`x = y = 1`

So we can conclude that there is one critical points:

`(1,1)`

Step 3 - Classify the critical points

In order to classify the critical points we perform a test similar to that of one variable calculus using the second partial derivatives and the Hessian Matrix.

`Delta = H f(x,y) = | ( f_(x x) \ \ f_(xy) ) , (f_(yx) \ \ f_(yy)) | = | ((partial^2 f) / (partial x^2),(partial^2 f) / (partial x partial y)), ((partial^2 f) / (partial y partial x), (partial^2 f) / (partial y^2)) | = f_(x x)f_(yy)-(f_(xy))^2`

Then depending upon the value of `Delta`:

`{: (Delta>0, "There is maximum if " f_(x x)<0),(, "and a minimum if " f_(x x)>0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :}`

Using custom excel macros the function values along with the partial derivative values are computed as follows: