Question

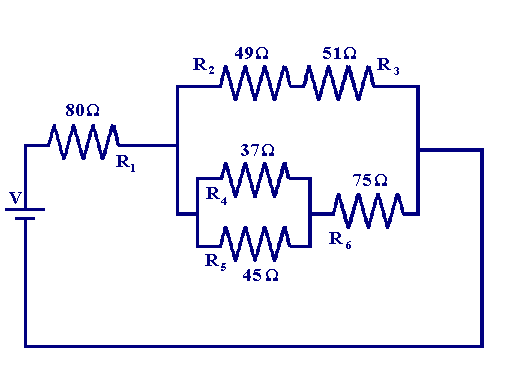
What are resistor combinations?

Answer 1

Resistor combinations combine series and parallel paths together in a single circuit.

This is a fairly simple combination circuit. To solve any combination circuit, simplify it down to a single series circuit. This is usually done most easily starting at the farthest point from the power source.

On this circuit, find the equivalent resistance of `R_2` and `R_3`, as if they were a single resistor connected to the others in series.

`1 / R_T = 1 / R_2 + 1 / R_3`
`1 / R_T = 1 / 30 + 1 / 50`
`1 / R_T = 8 / 150`
Take the reciprocal of each to get `R_T` out of the denominator:
`R_T = 150 / 8`
`R_T = 18.75 Omega`

Now add this to the `20 Omega` of `R_1` and the `20 Omega` of `R_2` to get a total resistance on this circuit of `58.75 Omega`.

Other circuits may be more complex, and you may have to do this several times - going back and forth between series and parallel - until this is simplified down to a simple series or parallel circuit.