What are some examples of physical chemistry?
1 Answer
Physical Chemistry is somewhat of a broad topic; it covers:
- Quantum chemistry
- Thermochemistry (Review + More)
- Kinetics (Review + More)
- Statistical mechanics
Since there are a fair few topics for one answer, I'll only provide two examples per topic. This is going to be a long answer, but you can focus on what you're looking for.
QUANTUM CHEMISTRY
Quantum chemistry is generally about trying to understand scenarios on the picoscopic scale, modeling systems in convenient mathematical representations and making the appropriate approximations.
Two examples of quantum chemistry are:
- Simple harmonic oscillator (two balls connected by an ideal [non-damped] spring)
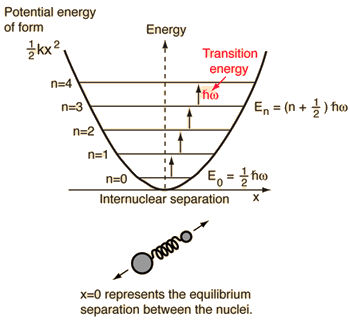
For this system, which we know from physics, we reduce it from a two-body classical problem to a one-body problem with relative coordinates and a reduced mass,
#mu = (m_1m_2)/(m_1 + m_2)# .This system focuses on understanding the elastic potential energy of the molecular bond.
- Rigid rotor (two balls connected by a rod, i.e. 100% stiff spring)
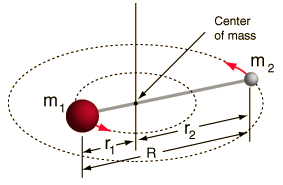
This system is a simplification, as all molecules have some form of bond stretching/vibration (you would understand why this simplification is OK, if you saw the math!).
However, it allows us to decompose this angular component of a two-body system and understand the rotational properties of the molecule.
THERMOCHEMISTRY
This looks at the macroscopic scale of heat flow, work, free energies, and so on. You've done this before in general chemistry somewhat, and this is reviewed and expanded upon.
Two examples are:
- Determining Thermodynamic Values from Measurable Quantities
What is chemistry if it isn't practical?
So, a common theme is to be able to perform derivations and express the main thermodynamic quantities (entropy, enthalpy, gibbs + helmholtz free energy, internal energy) in terms of natural variables like volume, temperature, and pressure.
For instance, one can calculate entropy from an isothermal expansion (
#DeltaT = 0, DeltaV > 0# ) by knowing#V_2# and#V_1# , or#P_2# and#P_1# , and that for a monatomic ideal gas:
#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#
- Ideal and Nonideal Non-Electrolyte/Electrolyte Solutions
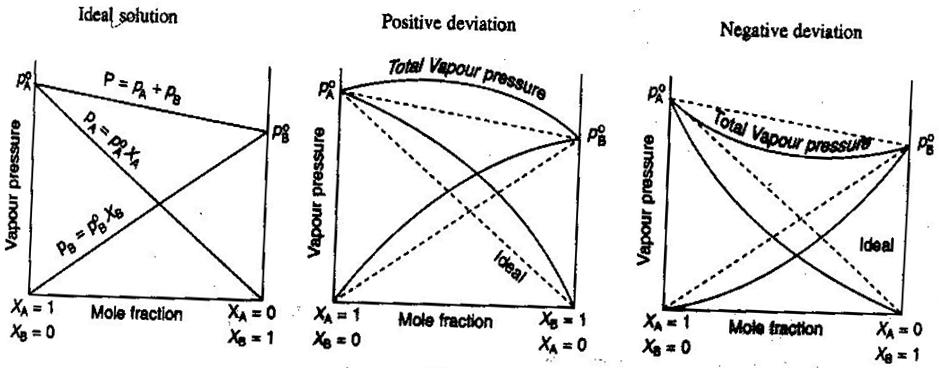
In general chemistry, we like to treat solutions ideally, so that volumes are additive, concentrations of strong electrolytes are straight
#"mol/L"# calculations, and so on. Some ways that solutions may not be ideal:
- The solution may expand or contract after being mixed.
- Ion pairing decreases the ionic strength of the solution and reduces the van't Hoff factor
#i# of the solute.- The escaping tendency of the solute alters its effective concentration (its activity).
KINETICS
You may have done this before in a general chemistry class, or maybe in high school. Physical chemistry expands on this a bit more by looking at reaction mechanisms and gas-phase dynamics in more detail.
Two examples:
- Steady-State approximation
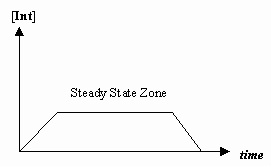
Sometimes the rate of the first mechanistic step is much slower than that of the second step, and we approximate that the concentration of the intermediate effectively doesn't change (
#(d[I])/(dt) = 0# ).That allows for the derivation of a rate law particular to a mechanism, and for us to express an "observed rate constant" in terms of the rate constants for the individual steps.
- Real Gas Laws
You may have been introduced to the van der Waals equation of state:
#[P + a(n^2/V^2)](V - nb) = nRT# Well, there are some others, like the Redlich-Kwong, the Peng-Robinson, and so on.
The basic idea is that they all work better for certain gases than others, but they all work to account for the real properties of gases instead of assuming everybody is an elastically-colliding inert point mass.
STATISTICAL MECHANICS
With statistical mechanics, we take a step back and look at the picoscopic world from a macroscopic perspective:
"What can be learned from a system if we think like a quantum chemist about a large collection of particles?"
Two examples:
- Equipartition Theorem
#<< K >> = N/2nRT = N/2 k_BT# ,where
#N# is the number of degrees of freedom for each type of motion (linear, rotational, vibrational, electronic, nuclear). Basically, it takes into consideration every type of motion in a molecule to estimate its average kinetic energy,#<< K >># .This only works at "high enough" temperatures. Usually, it is OK for translational and rotational motions, but it tends to overestimate vibrational contributions.
- The Microcanonical Partition Function
#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)# ,where:
#g_i# is the degeneracy of state#i# with energy#epsilon_i# .#N# is the total number of states available.Just like the wave function
#psi# specifies everything there is to know about a quantum mechanical system, the microcanonical partition function specifies how a molecule can distribute its available energy into the possible types of states (translational, rotational, vibrational, electronic, and nuclear).There exists a
#q# for each type of state:#q_(tr)# ,#q_(rot)# ,#q_(vib)# ,#q_(el ec)# , and#q_(n uc)# .From knowing each type of
#q# , the familiar thermodynamic quantities can be derived, such as entropy (#S# ), enthalpy (#H# ), Gibbs' free energy (#G# ), and so on, in terms of each kind of#q# .As a useful example, the absolute molecular entropy at ANY temperature in most cases can be calculated as:
#S/N = k_B ln (q/N)_"tot" + (<< epsilon >>_"tot")/T + k_B# ,where:
#k_B ~~ "0.695 cm"^(-1)"/K"# is the Boltzmann constant.#(q/N)_"tot" = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# is the total microcanonical partition function that includes all the possible types of states, and#N# is the total number of molecules considered.#<< epsilon >> = E/N# is the molecular energy, defined as#<< epsilon >> = k_BT^2((del ln (q"/"N)_"tot")/(del T))_V# .(Yes, this formula at
#"298.15 K"# allows you to calculate the same#S^@# that you see in your textbook Appendix!)An example of this formula in use can be found here.

