What are the absolute extrema of #f(x)=5x^7 - 7x^5 - 5 in[-oo,oo]#?

Question

2689 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-26T16:17:47

There are not absolute extrema because #f(x)# unbounded
There are local extrema:

LOCAL MAX: #x=-1#
LOCAL MIN: #x=1#
INFLECTION POINT #x=0#

There are not absolute extrema because

#lim_(x rarr +-oo) f(x) rarr +-oo#

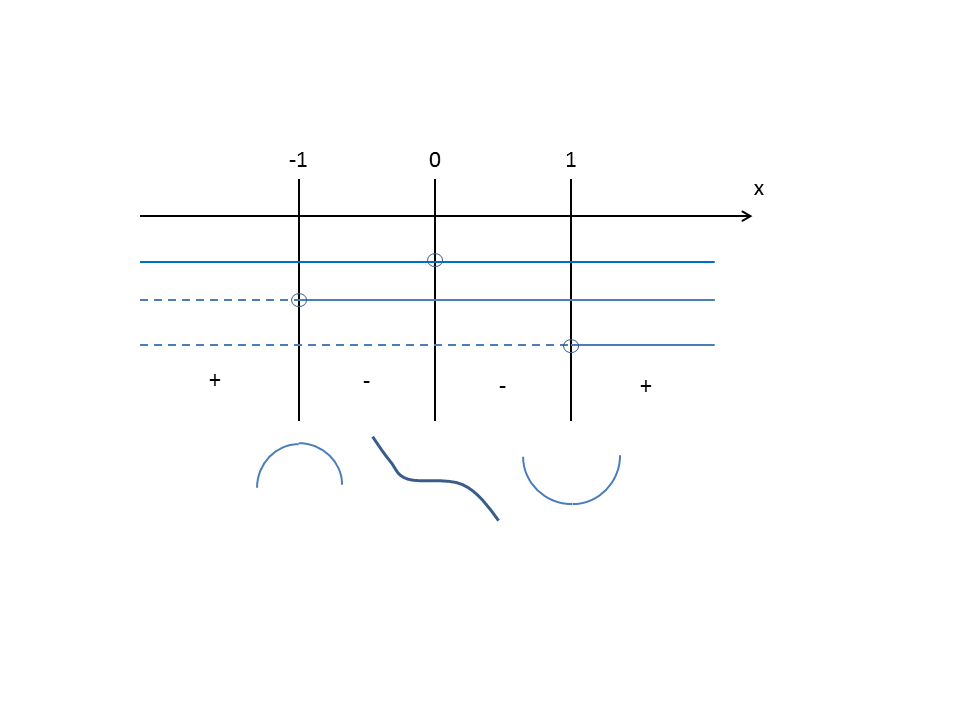
You could find local extrema, if any.

To find #f(x)# extrema or critical poits we have to computate #f'(x)#

When #f'(x)=0 => f(x)# has a stationary point (MAX, min or inflection point).
Then we have to find when:

#f'(x)>0 => f(x)# is increasing
#f'(x)<0 => f(x)# is decreasing

Therefore:

#f'(x)=d/dx(5x^7-7x^5-5)=35x^6-35x^4+0=35x^4(x^2-1)#

#:.f'(x)=35x^4(x+1)(x-1)#

#color(green)cancel(35)x^4(x+1)(x-1)=0#

#x_1=0#
#x_(2,3)=+-1#

#x^4>0# #AAx#
#x+1>0 => x> -1#
#x-1>0 => x>1#

Drawing the plot, you'll find

enter image source here

#f'(x)>0 AAx in (-oo,-1)uu(1,+oo)#

#f'(x)<0 AAx in(-1,1)#

#:.f(x)# increasing #AA x in (-oo,-1)uu(1,+oo)#
#:.f(x)# decreasing #AA x in (-1,1)#

#x=-1=>#LOCAL MAX
#x=+1=># LOCAL MIN
#x=0=># INFLECTION POINT

graph{5x^7-7x^5-5 [-16.48, 19.57, -14.02, 4]}

Answer 2 · 2016-01-26T18:00:38

That function has no absolute extrema.

#lim_(xrarroo)f(x) = oo# and #lim_(xrarr-oo)f(x) = -oo#.

So the function is unbounded in both directions.