What are the absolute extrema of # f(x)= cos(1/x)−xsin(1/x) in [-1/pi,1/pi]#?
1 Answer
Jul 2, 2017
An infinite number of relative extrema exist on
Explanation:
First, let's plug the endpoints of the interval
Next, we determine the critical points by setting the derivative equal to zero.
Unfortunately, when you graph this last equation, you get the following
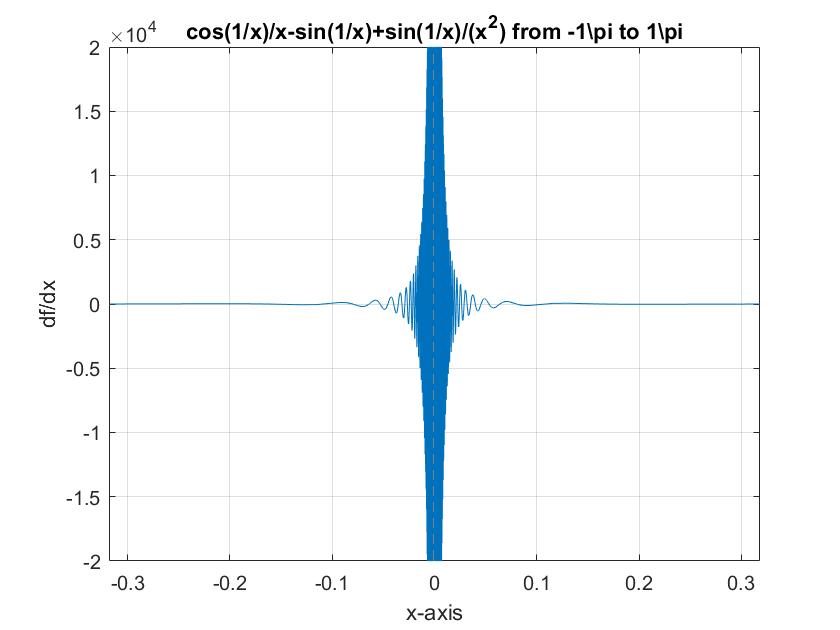
Because the graph of the derivative has an infinite number of roots, the original function has an infinite number of local extrema. This can also be seen by looking at the graph of the original function.
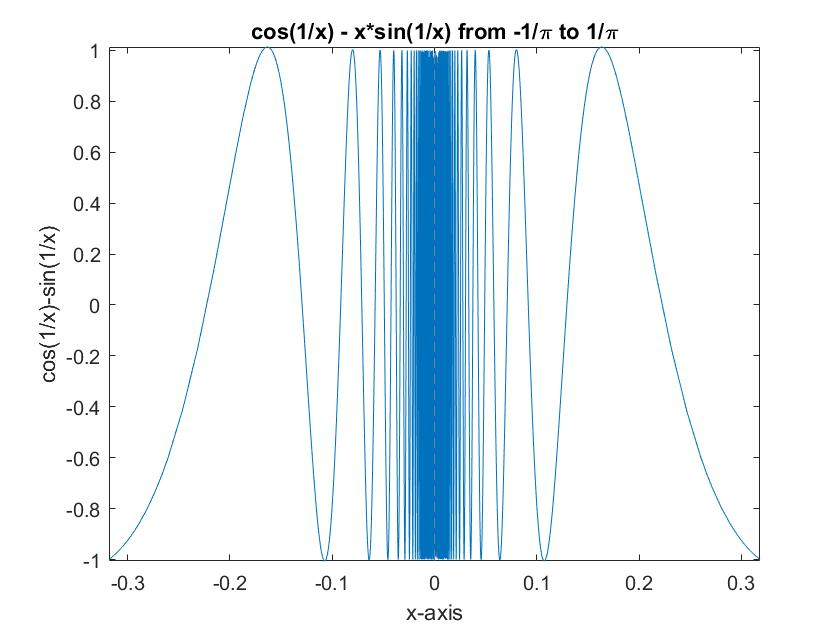
However, none of them ever surpass
