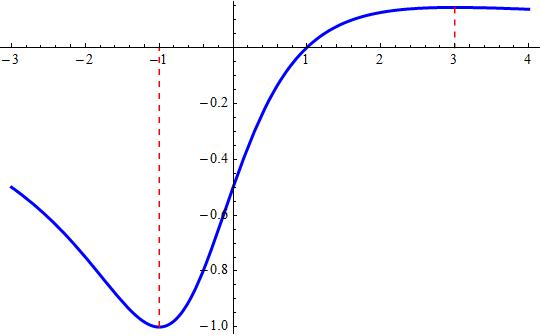
What are the absolute extrema of #f(x)=(x-1)/(x^2+x+2) in[oo,oo]#?

Question

1226 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-10-11T15:55:56

At #x=-1# the minimum
and at #x=3# the maximum.

#f(x)=(x-1)/(x^2+x+2)# has stationary points characterized by

#(df)/(dx) = -((x-3) (1 + x))/(2 + x + x^2)^2=0# so they are at

#x=-1# and #x=3#

Their characterization is made analyzing the signal of

#(d^2f)/(dx^2) = (2 (x ((x-3) x-9))-1)/(2 + x + x^2)^3# at those points.

#(d^2f)/(dx^2)(-1)=1 > 0-># relative minimum
#(d^2f)/(dx^2)(3)=-1/49 < 0-># relative maximum.

Attached the function plot.

enter image source here