Question

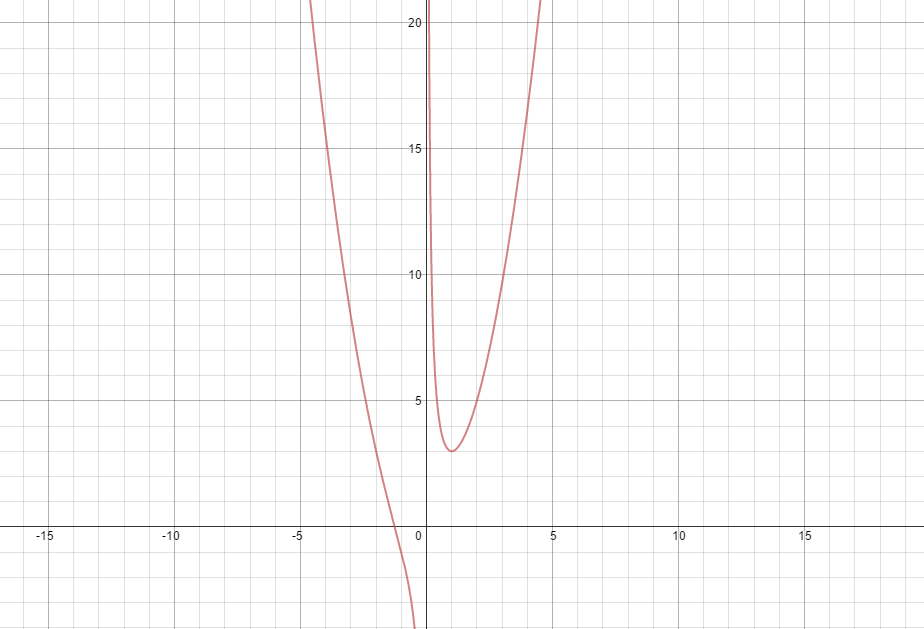
What are the absolute extrema of `f(x)= x^(2)+2/x` on the interval [1,4]?

Answer 1

We need to find the critical values of `f(x)` in the interval `[1,4]`.

Hence we calculate the roots of the first derivative so we have

`(df)/dx=0=>2x-2/x^2=0=>2x^2(x-2)=0=>x=2`

So `f(2)=5`

Also we find the values of `f` at the endpoints hence

`f(1)=1+2=3`

`f(4)=16+2/4=16.5`

The largest function value is at `x=4` hence `f(4)=16.5` is the absolute maximum for `f` in `[1,4]`

The smallest function value is at `x=1` hence `f(1)=3` is the absolute minimum for `f` in `[1,4]`

The graph of `f` in `[1,4]` is