Question

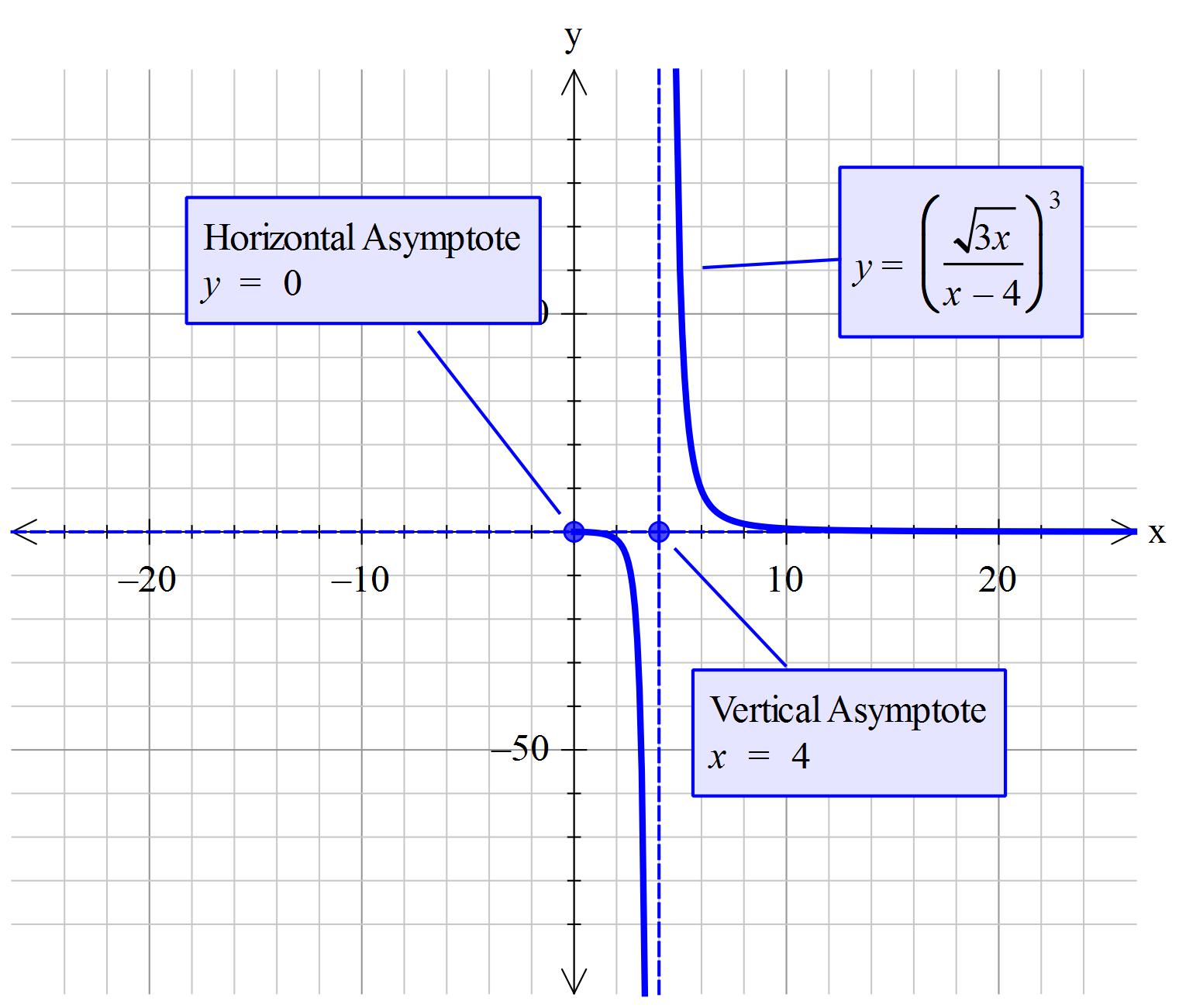
What are the asymptote(s) and hole(s), if any, of `f(x) =(sqrt(3x)/(x-4))^3`?

Answer 1

Asymptotes are `x=4" and "y=0`

Explanation:

Write as:`" "f(x)=(3xsqrt(3x))/((x-4)^3)`

`color(blue)("Point 1")`

We know that the function will be undefined as the denominator approaches zero.

Thus `lim_(x->4) f(x) =lim_(x->4) (3xsqrt(3x))/((x-4)^3) -> (12sqrt(12))/0`

`color(blue)("This is undefined" => x=4 " is an asymptote")`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Point 2")`

The denominator has `x^3` as the most significant figure.
Whilst the numerators most significant figure is `xsqrt(x)`

Note that `xsqrt(x) < x^3` so as the denominator 'grows' much faster
than the numerator `lim_(x->+-oo) f(x)" tends to "0`

`color(blue)("Thus " y=0" is an asymptote")`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~