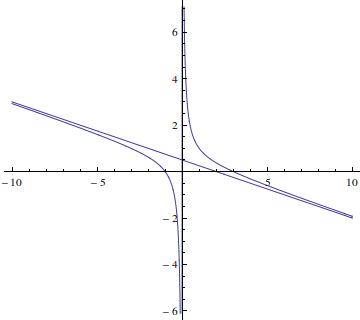
In a polynomial fraction #f(x) = (p_n(x))/(p_m(x))# we have:
#1)# vertical asymptotes for #x_v# such that #p_m(x_v)=0#
#2)# horizontal asymptotes when #n le m#
#3)# slant asymptotes when #n = m + 1#
In the present case we have #x_v = 0# and #n = m+1# with #n = 2# and #m = 1#
Slant asymptotes are obtained considering #(p_n(x))/(p_{n-1}(x))
approx y = a x+b # for large values of #abs(x)#
In the present case we have
#(p_n(x))/(p_{n-1}(x)) = (x^2-2x-3)/(-4x)#
#p_n(x) = p_{n-1}(x)(a x+b)+r_{n-2}(x)#
#x^2-2x-3 =(-4x)(a x + b) + c#
equating coefficients
#{
(-3 - c=0),
(-2 + 4 b=0),
(1 + 4 a=0)
:}#
solving for #a,b,c# we get #{a = -(1/4), b = 1/2, c = -3}#
and substituting
#y = -x/4+1/2 #