What are the asymptotes for #y=3/(x-1)+2# and how do you graph the function?
1 Answer
Vertical Asymptote is at
Horizontal Asymptote is at
Graph of the rational function is available with this solution.
Explanation:
We are given the rational function
We will simplify and rewrite
Hence,
Vertical Asymptote
Set the denominator to Zero.
So, we get
Hence,
Vertical Asymptote is at
Horizontal Asymptote
We must compare the degrees of the numerator and denominator and verify whether they are equal.
To compare, we need to deal with lead coefficients.
The lead coefficient of a function is the number in front of the term with the highest exponent.
If our function has a horizontal asymptote at
where
Hence,
Horizontal Asymptote is at
Graph of the rational function with the horizontal asymptote and the vertical asymptote can be found below:
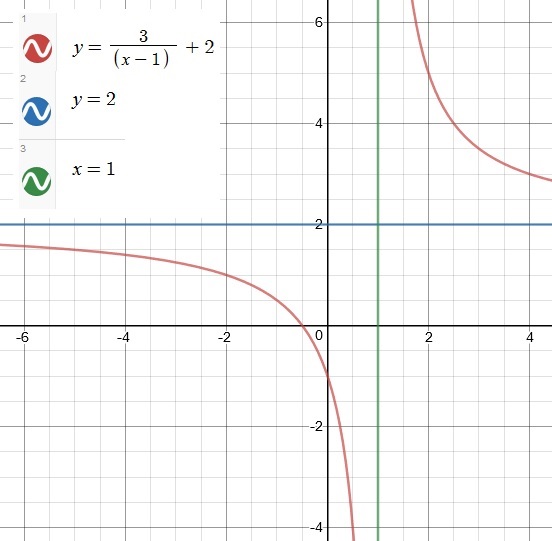
I hope you find this solution with the graph useful.

