Question

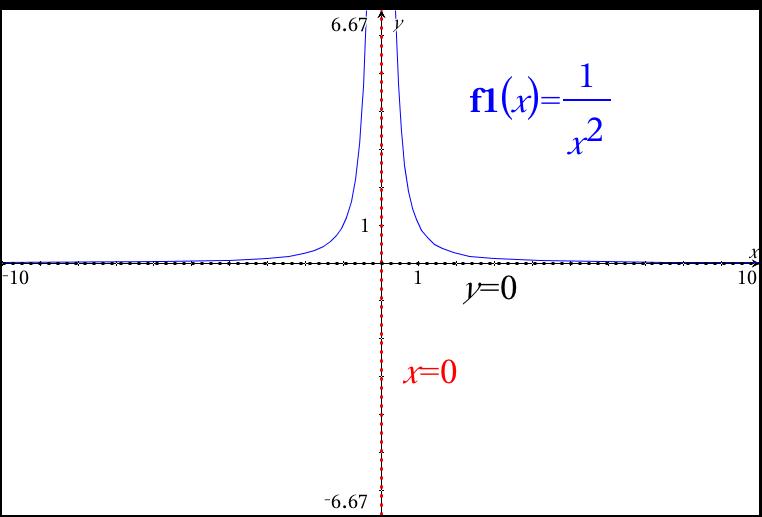
What are the asymptotes of `y=1/x^2`?

Answer 1

Vertical asymptotes for rational functions are found by setting the denominator equal to 0. This also helps to find the domain. The domain can NOT contain that number! For this function, `x^2!= 0`
so x = 0 is the equation of the vertical asymptote, and 0 must be left out of the domain: `(-infty,0)U(0,infty)` in interval notation.

Horizontal asymptotes are found by substituting in large positive and negative values into the function. f(1000) or f(1000000) can help to determine where the function "ends" are heading. In this case, `1/(1000)^2` or `1/(1000000)^2` will get pretty close to 0. (this is called a limit) Your horizontal asymptote will be at y = 0. This also helps to determine the domain of this function, since `y!=0`. In interval notation, `(-infty,0)U(0,infty)` .

The graph below shows you the function (in blue), and the asymptotes as dotted lines labeled with their equations.