Transformations of the Reciprocal Function
Key Questions
-
Answer:
An element(point, line, plane or any other geometric, complex or whatever figure) is said to undergo a transformation when ever one or more of its properties are changed.
Explanation:
A transformation just a rule; its more like a function. It takes an object and returns that object's image.
Transformations are done using: functions, matrices, complex numbers etc.
What we call object can be a point, a line etc. The basic fact about all objects is that object haves properties.
For example: The point
#A(3,2)# has only the property of position(in a Cartesian coordinate system).Once you change point
#A# 's position to let's say#B(6,4)# by a particular procedure, we say you have transformed point#A# to be point#B# .And in which case the object is
#A(x,y)# and the image is#B(6,4)# Our transformation could be the matrix:
#({:(2" "0),(2" "0):})# Proof : Because
#({:(2" "0),(0" "2):})xx({:(3),(2):})=({:(6),(4):})# -
Answer:
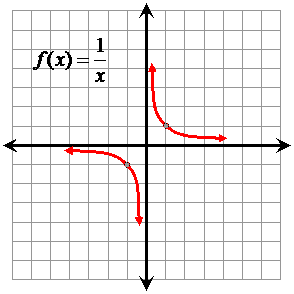
The basic reciprocal function is
#1/x# Explanation:
The graph looks like:
graph{1/x [-10, 10, -5, 5]}