What are the critical points of #f(x,y) = e^(x^3) + y^3 - e^(xy)#?
1 Answer
Oct 31, 2015
The critical points are
Explanation:
The partial derivatives are:
If you set these both equal to 0, the resulting system of equations clearly has
The first one is a saddle point and the second one is a local minimum.
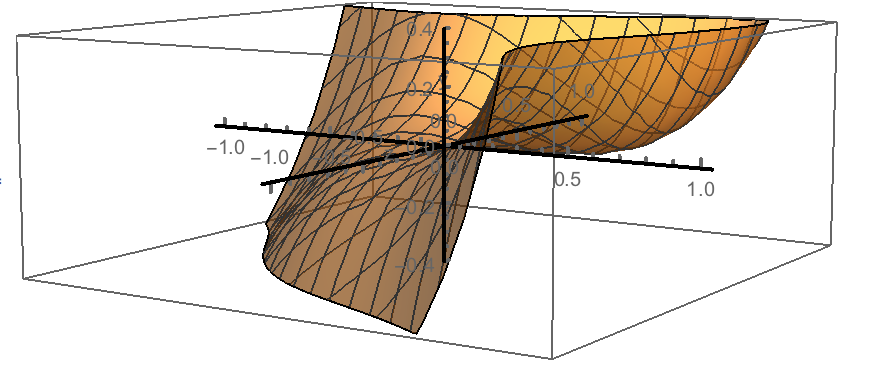
Below is a 3-dimensional picture of the graph of this function. The positive