What are the crystal field Splitting energy and the spin only moment in Bohr Magneton for the complex #K_3[Fe(CN)_6]# ?
How to calculate this?
How to calculate this?
2 Answers
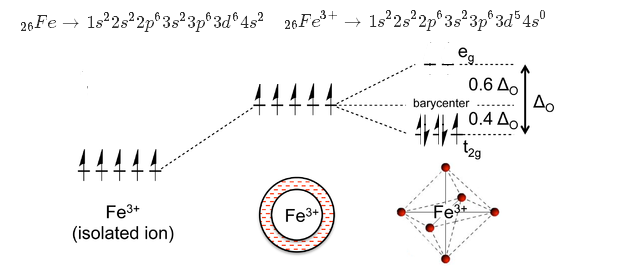
Electronic configuration of
Electronic configuration of
In
Here the crystal field Splitting energy
The spin only moment
So
The field-splitting energy is
In
With six cyanide ligands, which are known to be great
- Stabilization of the triply-degenerate
#bb(t_(2g))# #3d# molecular orbitals by the back-donation of#pi# electrons from the metal simultaneously into the cyanide ligand's#2p_x# and#2p_y# orbitals (#3d_(xz) -> 2p_x# ,#3d_(yz) -> 2p_y# ). - Destabilization of the doubly-degenerate
#bb(e_g)# #3d# molecular orbitals by the donation of#sigma# electrons from the cyanide ligand's#sp# orbitals into the metal's#3d_(z^2)# (axial) and#3d_(x^2 - y^2)# (equatorial) atomic orbitals (#sp -> 3d_(z^2)# ,#sp -> 3d_(x^2 - y^2)# ).
Both of these work to increase the overall ligand field splitting energy,
Since there are six ligands around iron, we have an octahedral complex, with a splitting energy of
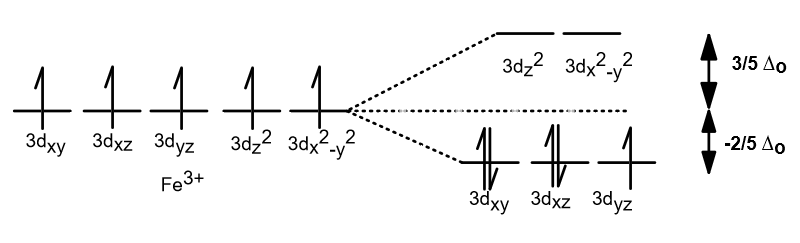
The fact that the two previously-mentioned effects are working in coincidence to increase
These make the transition-metal complex a low-spin complex, since as a general rule, it is difficult for the electrons to populate the antibonding
The ligand-field splitting energy is calculated as each electron in an occupied orbital multiplied by the relevant splitting energy with respect to the free-ion energy. Therefore, we have:
#color(blue)(E_"splitting") = (2 + 2 + 1)xx(-2/5Delta_o) = color(blue)(-2Delta_o)#
The spin-only magnetic moment,
#bb(mu_S = gsqrt(S(S+1)))# ,
where
From left to right, we have a total spin of
#color(blue)(mu_S) = 2.00023sqrt(1/2(1/2 + 1))#
#=# #color(blue)("1.732 BM")#


