#f(x,y) = e^y(y^2-x^2)#
so the sationary points are determined by solving
#grad f(x,y) = vec 0#
or
#{
(-2 e^y x = 0), (2 e^y y + e^y (-x^2 + y^2) = 0)
:}#
giving two solutions
#((x=0,y=0),(x=0,y=-2))#
Those points are qualified using
#H = grad(grad f(x,y))#
or
#H =((-2 e^y, -2 e^y x),(-2 e^y x, 2 e^y + 4 e^y y + e^y (-x^2 + y^2))) #
so
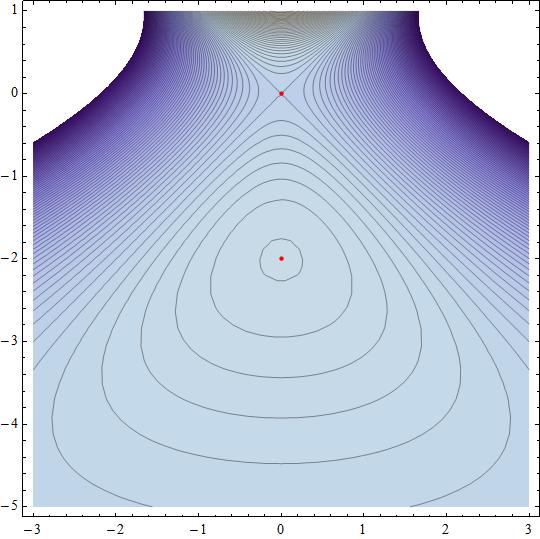
#H(0,0) = ((-2, 0),(0, 2))# has eigenvalues #{-2,2}#. This result qualifies point #{0,0}# as a saddle point.
#H(0,-2)=((-2/e^2, 0),(0, -2/e^2))# has eigenvalues #{-2/e^2, -2/e^2}#. This result qualifies point #{0,-2}# as a local maximum.
Attached the #f(x,y)# contour map near the points of interest