Question

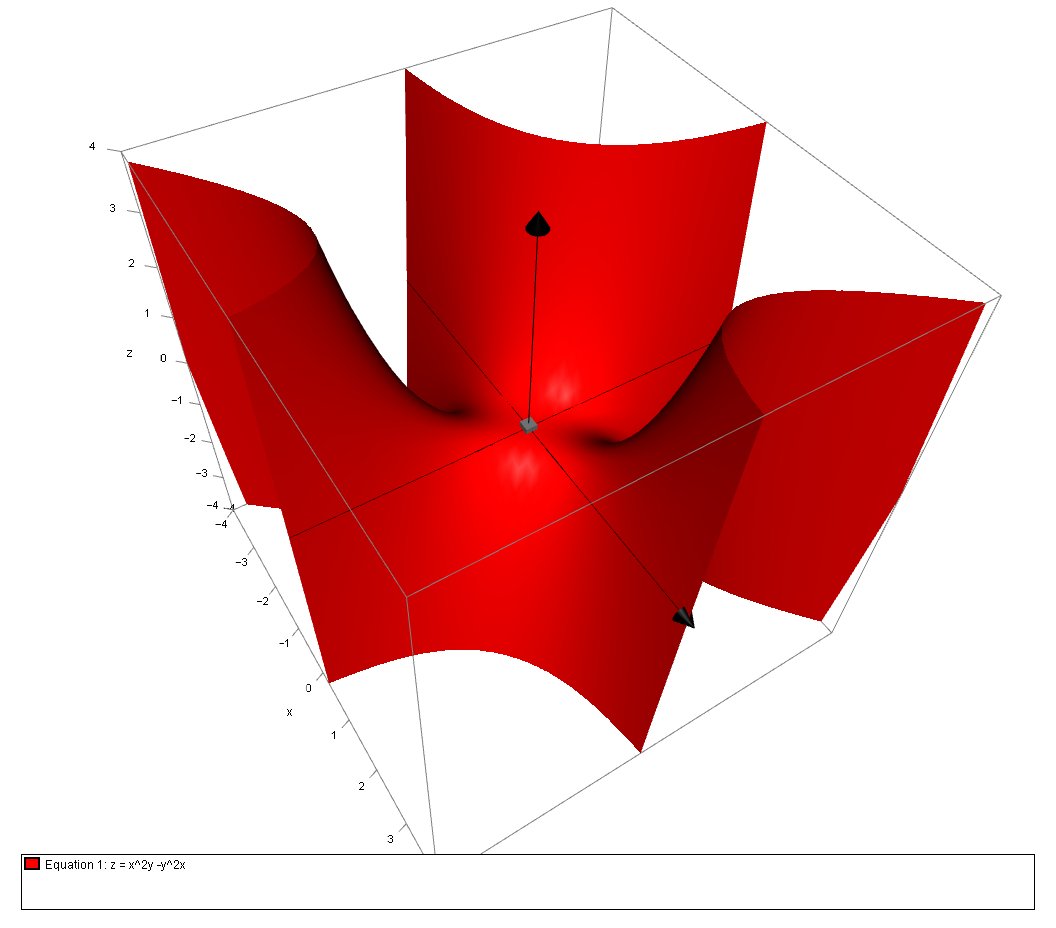
What are the extrema and saddle points of `f(x,y) = x^2y-y^2x`?

Answer 1

Saddle point at the origin.

Explanation:

We have:

`f(x,y) = x^2y -y^2x`

And so we derive the partial derivatives. Remember when partially differentiating that we differentiate wrt the variable in question whilst treating the other variables as constant. And so:

`(partial f) / (partial x) = 2xy-y^2 \ \ \` and `\ \ \ (partial f) / (partial y) = x^2-2yx`

At an extrema or saddle points we have:

`(partial f) / (partial x) = 0 \ \ \` and `\ \ \ (partial f) / (partial y) = 0 \ \ \` simultaneously:

i.e. a simultaneous solution of:

`2xy-y^2 = 0 => y(2x-y) = 0 => y=0, x=1/2y`
`x^2-2yx = 0 => x(x-2y) = 0 => x=0, x=1/2y`

Hence there is only one critical point at the origin `(0,0)`. To establish the nature of the critical point, analysts of the multi-variable Taylor Series is required and the following test results:

`Delta = (partial^2 f) / (partial x^2) \ (partial^2 f) / (partial y^2) - {(partial^2 f) / (partial x partial y)}^2 < 0 =>` saddle point

So we calculate the second partial derivatives:

`(partial^2f) / (partial x^2) = 2y \ \ \`;`\ \ \ (partial^2f) / (partial y^2) = -2x \ \ \` and `\ \ \ (partial^2 f) / (partial x partial y) =2x-2y`

And so when `x=0, y=0` we get:

`Delta = (0)(0)-{0-0}^2 = 0`

Which means that the standard saddle test is inclusive and further analysis is required. (This would typically involve looking at the signs of the function across various slices, or looking at the third partial derivative test which is beyond the scope of this question!).

We can also look at the 3D plot and draw a quick conclusion that the critical point appears to correspond to a saddle point: