What are the extrema of #f(x)=-sinx-cosx# on the interval #[0,2pi]#?
1 Answer
Nov 8, 2015
Since
Explanation:
Solve:
Now, either use the unit circle or sketch a graph of both functions to determine where they are equal:
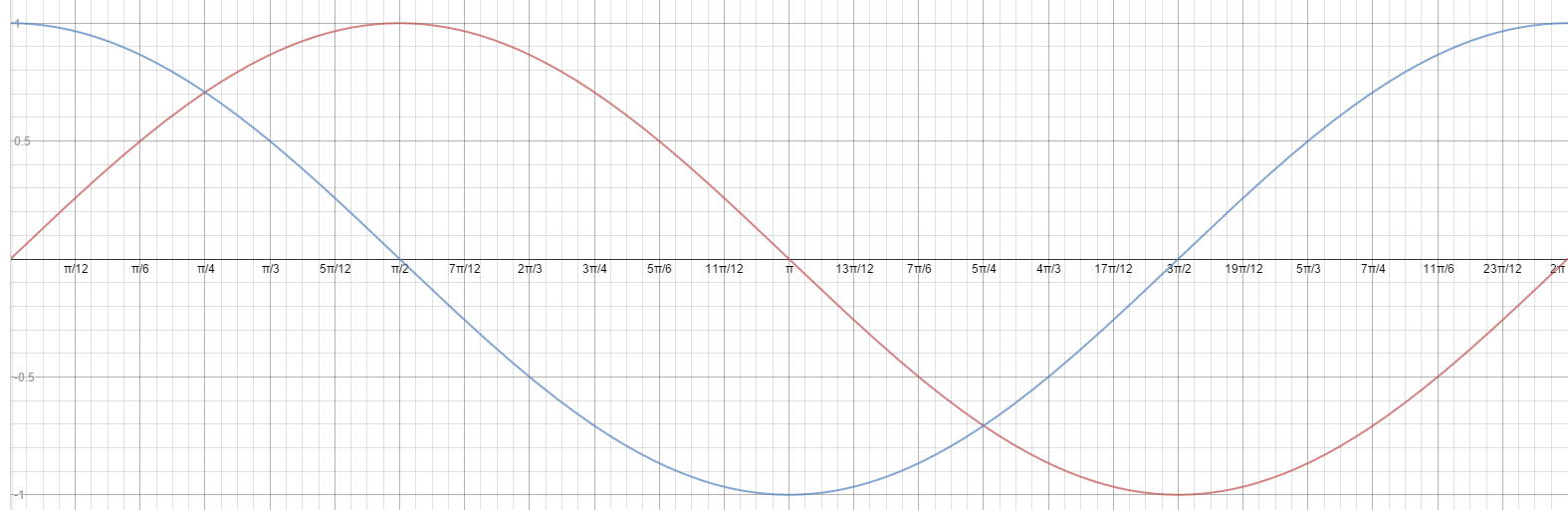
On the interval
hope that helps

