What are the global and local extrema of #f(x)=x^3-x^2-x# ?

Question

1344 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-31T07:01:19

There is a maxima at #x=-1/3#
There is a minima at #x=1#

Given -

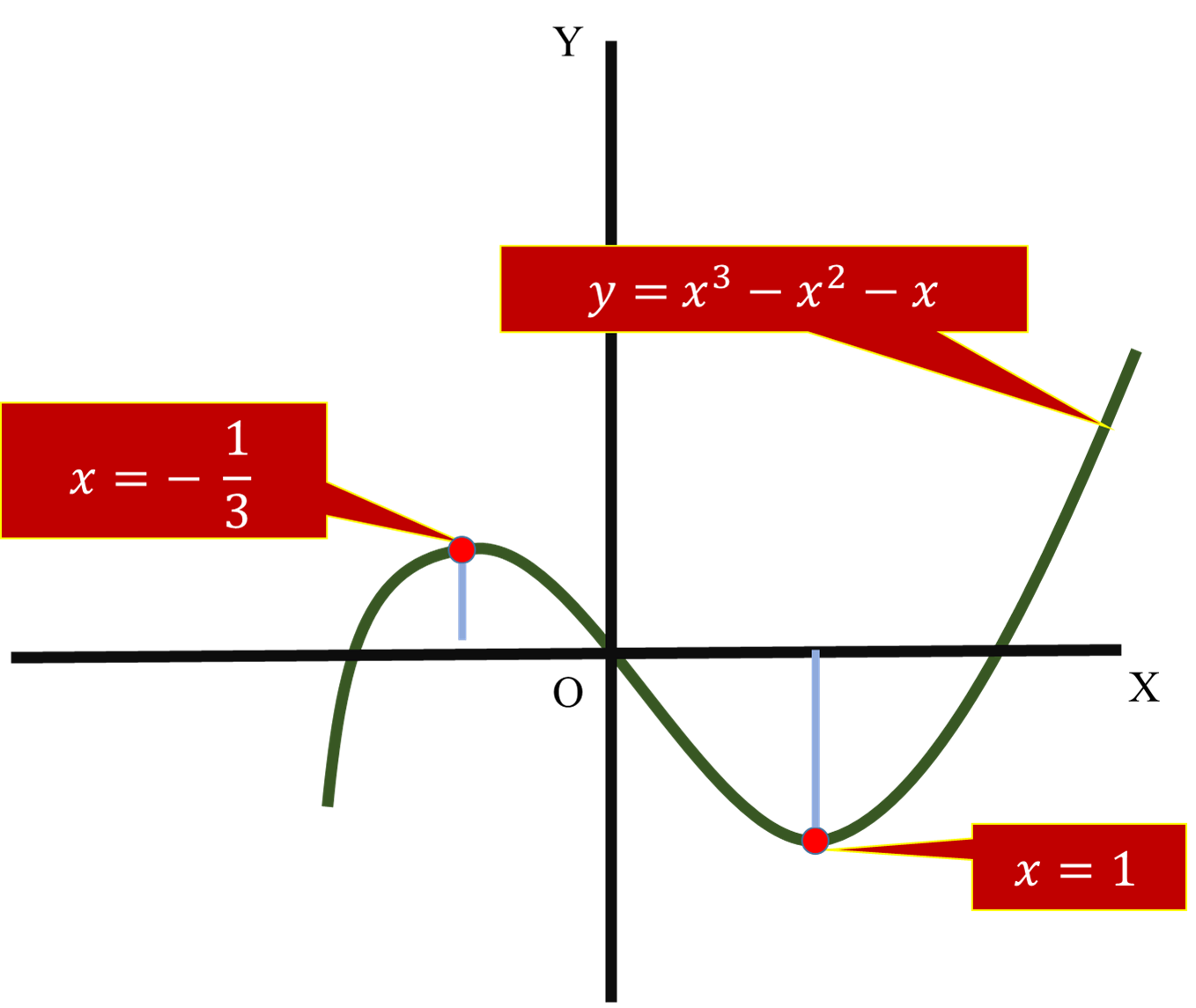
#y=x^3-x^2-x#
#dy/dx=3x^2-2x-1#
#(d^2y)/(dx^2)=6x-2#

Set the first derivative equal to zero

#dy/dx=0 =>3x^2-2x-1=0#

#3x^2-3x+x-1=0#

#3x(x-1)+1(x-1)=0#
#(3x+1)(x-1)=0#
#3x=-1#
#x=-1/3#
#x-1=0#
#x=1#

At #x=-1/3#

#(d^2y)/(dx^2)=6(-1/3)-2=-2-2=-4<0#

There is a maxima at #x=-1/3#

#(d^2y)/(dx^2)=6(1)-2=6-2=4>0#

There is a minima at #x=1#

Look at the graph