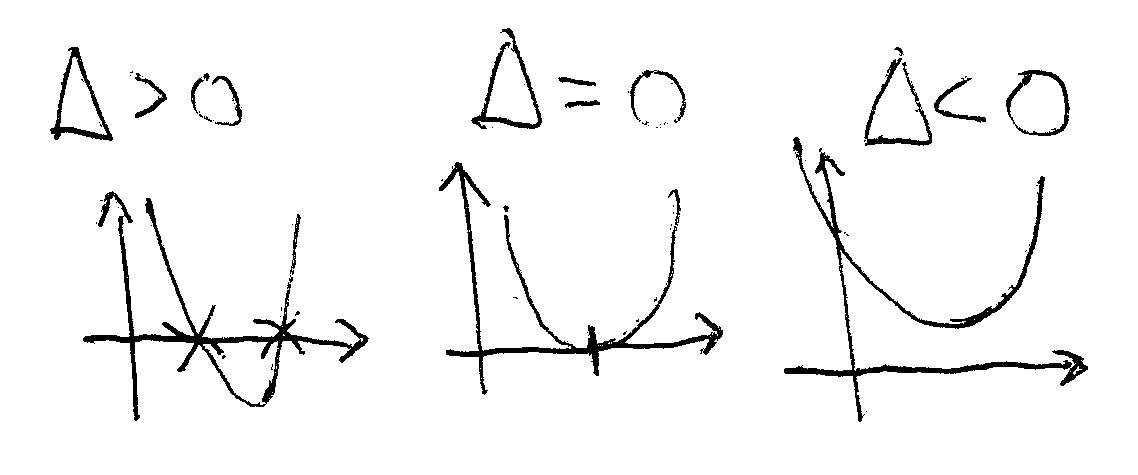Question

What are the important features of the graphs of quadratic functions?

Answer 1

A quadratic function has the general form:
`y=ax^2+bx+c`

(where `a,b and c` are real numbers) and is represented graphically by a curve called PARABOLA that has a shape of a downwards or upwards U.
The main features of this curve are:
1) Concavity: up or down. This depends upon the sign of the real number `a`:

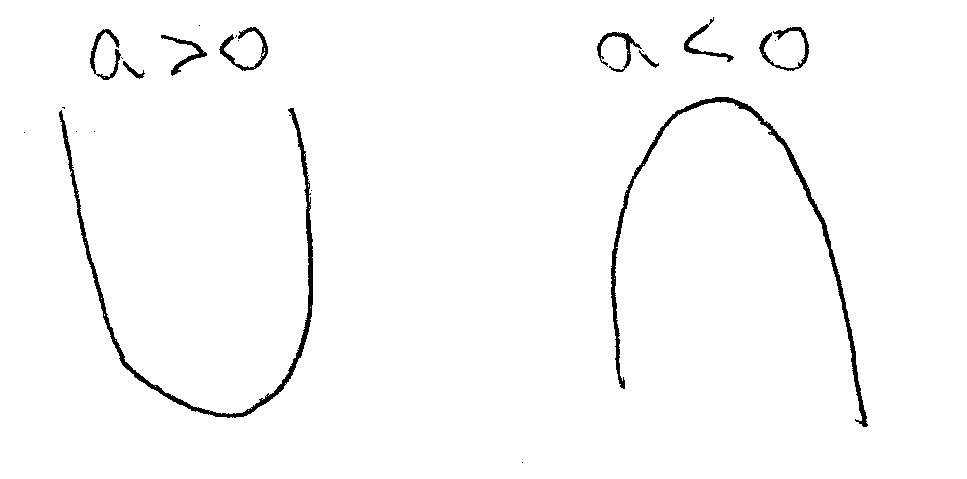
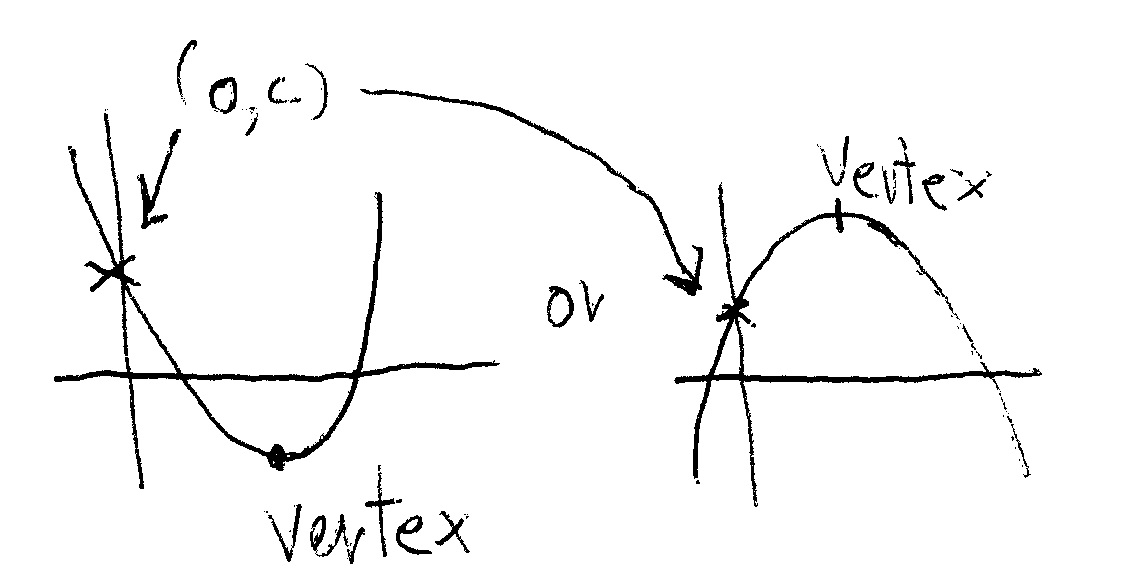
2) Vertex. The vertex is the highes or lowest point of the parábola.
the coordinates of this point are:
`x=-b/(2a)` and `y=-Delta/(4a)`
Where `Delta=b^2-4ac`

3) point of intercept with the y axis. This is the point where the parábola crosses the y axis and has coordinates: `(0,c)`

4) Possible points of intercept with the x axis (there also can be none). These are the points where the parábola crosses the x axis.
They are obtained by putting y=0 and solving for x the 2nd degree equation: `ax^2+bx+c=0`, which will give the x coordinates of these points (2 solutions)
Depending on the discriminant `Delta=b^2-4ac` if it is <0 the parábola does not cross the x axis.