Question

What are the local extrema, if any, of `f (x) =xe^(x^3-7x)`?

Answer 1

`(0.14414, 0.05271)` is a local maximum

`(1.45035, 0.00119)` and `(-1.59449, -1947.21451)` are the local minimums.

Explanation:

.

`f(x)=y=xe^(x^3-7x)`

`dy/dx=x(3x^2-7)e^(x^3-7x)+e^(x^3-7x)=e^(x^3-7x)(3x^3-7x+1)=0`

`e^(x^3-7x)=0, :. 1/e^(7x-x^3)=0, :. e^(7x-x^3)=-oo, :. x=oo`

This does not qualify as a local extremum.

`3x^3-7x+1=0`

To solve for the roots of this cubic function, we use the Newton-Raphson method:

`x_(n+1)=x_n-f(x_x)/(f'(x_n))`

This is an iterative process that will take us close and closer to the root of the function. I am not including the lengthy process here but having arrived at the first root, we can perform long division and solve the remaining quadratic easily for the other two roots.

We will get the following roots:

`x=0.14414, 1.45035, and -1.59449`

We now perform a first derivative test and try values to the left and right of each root to see where the derivative is positive or negative.

This will tell us which point is a maximum and which a minimum.

The result will be as follows:

`(0.14414, 0.05271)` is a local maximum

`(1.45035, 0.00119)` and `(-1.59449, -1947.21451)` are the local minimums.

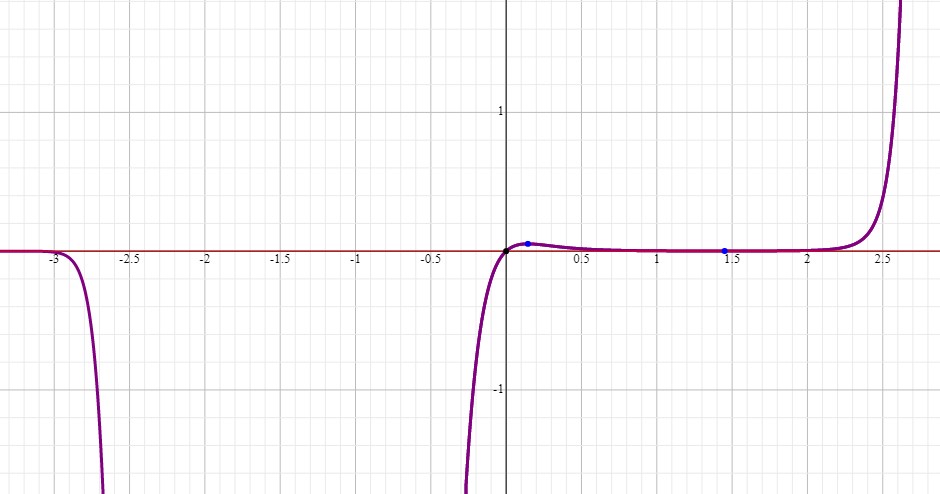
You can see one of the minimums in the graph below:

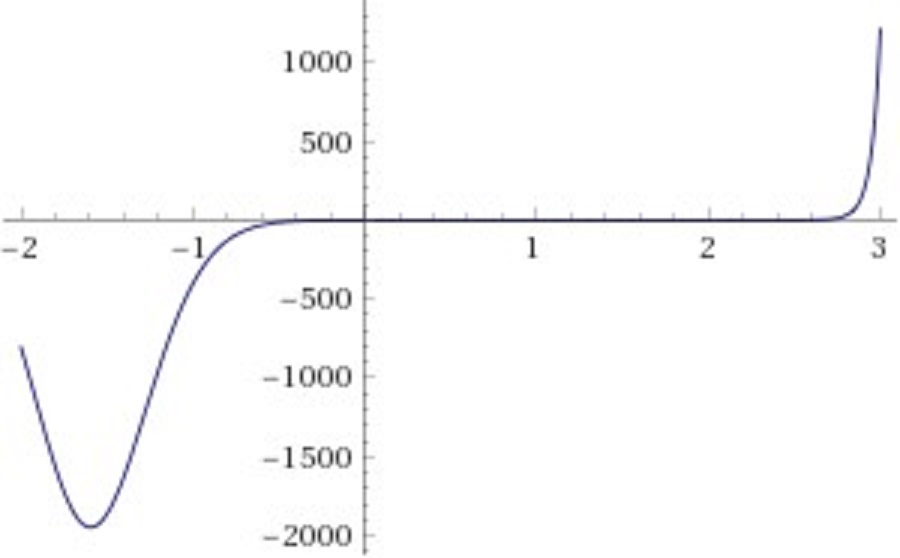
The following view shows the maximum and the other minimum: