What are the points of inflection, if any, of #f(x)=8xe^x-e^(x^2-4x) #?
2 Answers
I couldn't find any.
Explanation:
We first find the critical points by evaluating the first derivative.
Critical point when
Take natural logs of both sides:
Using rules of logs we can rewrite as
Because exp and ln are inverse operators, they cancel out:
Rearranging:
Take exponentials of both sides, we can also simplify the fraction on the right hand side:
This algebra isn't getting anywhere. We know that there is a critical point where f'(x) = 0. This point will be the root of this expression. We will have to find this root numerically. We define a new function
and will use the Newton-Raphson (NR) method to find the root of this function. NR is an iterative scheme based on an initial guess designed to find the zeroes of a function f such that f(r) = 0. It is given by
and will have
Hence
We will start with initial guess
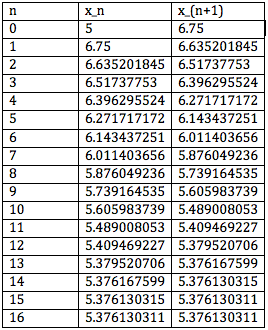
We end up with
I'm going to shamelessly admit that I used Wolfram Alpha to do the second derivative of the original function because I'm lazy and it's just simple stuff, applied again and again.
Subbing in our "r" value gives:
I'm not getting any other roots despite using various other root finding methods, although looking at the plot there does seem to be a point of inflection. I can't find it so I'm going to tentatively say that there is no point of inflection, I'll happily eat my hat if someone can prove otherwise though!
I am just following Euan, in the search for point of inflexion , if any., See the explanation.
Explanation:
Please check whether there is a negative root for f''(x)=0, near 0. If so, Euan could use Newton Raphson method and approximate this root, for the point of inflexion x. It is relevant that f'(x) need not be 0, at a point of inflexion. For example, if f(x) = sin x, x=0 is a (tangent-crossing-the-curve) point of inflexion. f'(0)=cos 0 =1.

