What are the points of inflection, if any, of #f(x)=x^4-x^2+5 #?
1 Answer
Dec 24, 2015
Inclection points are
Explanation:
For
For
For
Therefore inclection points are
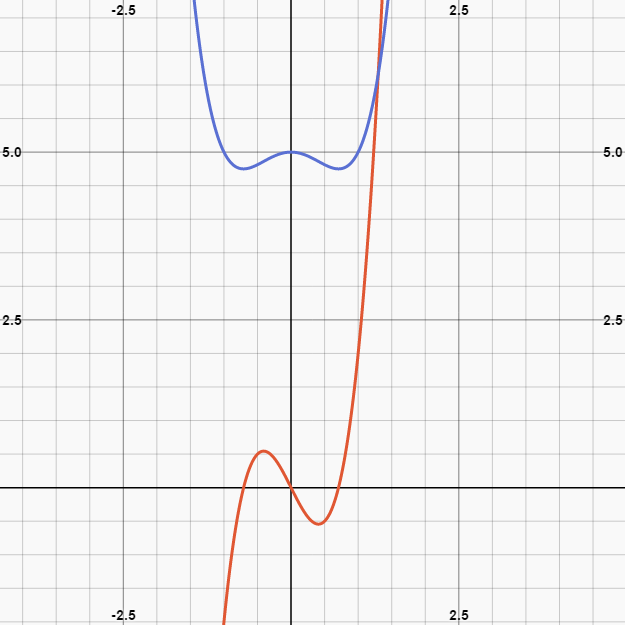
Inclection points are
For
For
For
Therefore inclection points are
