What are the points of inflection, if any, of #f(x)= x^5 -7 x^3- x^2-2 #?
1 Answer
Feb 6, 2016
We can't easily find exact locations, but there are three inflection points at roughly x = -1.4, 0, and 1.5. Graphs below.
Explanation:
To find inflection points we want the concavity to change from concave up to concave down, usually the second derivative is zero (or undefined) there.
Set f''(x) = 0 (since for polynomials the derivatives are never undefined):
This f''(x) = 0 equation doesn't factor or have rational roots, but does have three solutions, at about -1.42, -0.04, and 1.47. (I used tables of values to zoom in on the roots.)
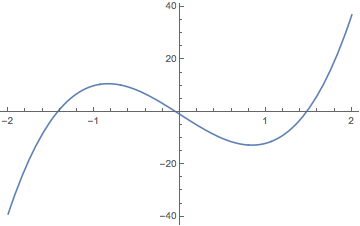
The original function with its three inflection points:
// dansmath \\ strikes again!

