What are the points of inflection of f(x)= x/e^(x^2) - x^2e^x ?
1 Answer
You will need to find successive derivatives, specifically f'(x) and f"(x). You will also need technology to visualize these points of inflection. The TI89 is perfect for such applications.
You won't be able to algebraically ( * exact * ) solve for the roots to f"(x)=0.
Explanation:
Do this:
(1) Find f"(x)
(2)Set f"(x) = 0
Now, you will need technology (TI89, 200, Maple, etc.) for finding the roots to the above equation. You can also use iterative* * root approximation methods like Newton's Method.
You should also construct * concavity/increasing/decreasing * tables to help "zero in" (he he) on the points of inflection.
(3) Recall that points of inflection are points of the form (x,f(x)) on the graph of f(x) where concavity changes.
There are (I believe, upon initial inspection) infinitely many points of inflection. Here are 4 points for
or
or
or
This can be confirmed with the following TI89 screenshots.
Again though, you need to find all derivatives and subsequently show that you can't algebraically arrive at the roots for the second derivative. Technology shines, here.
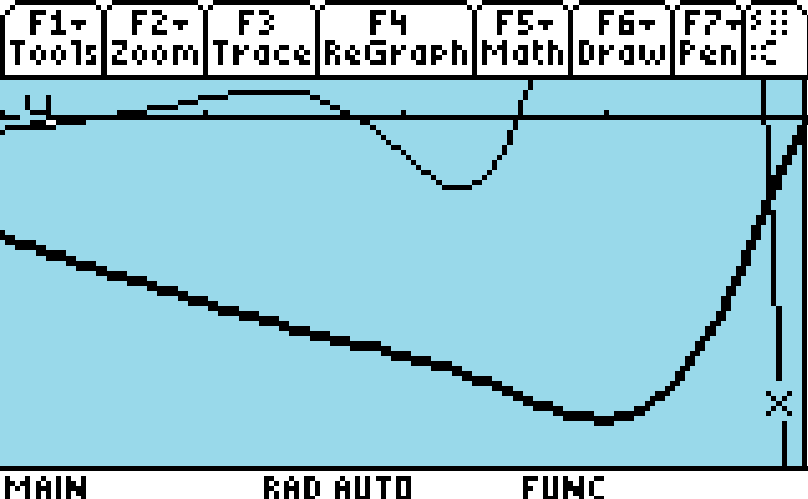
This first graph shows both f"(x) and f(x) in the same plane. Observe all 4 - x intercepts (roots) for f"(x) (drawn with the skinnier line).
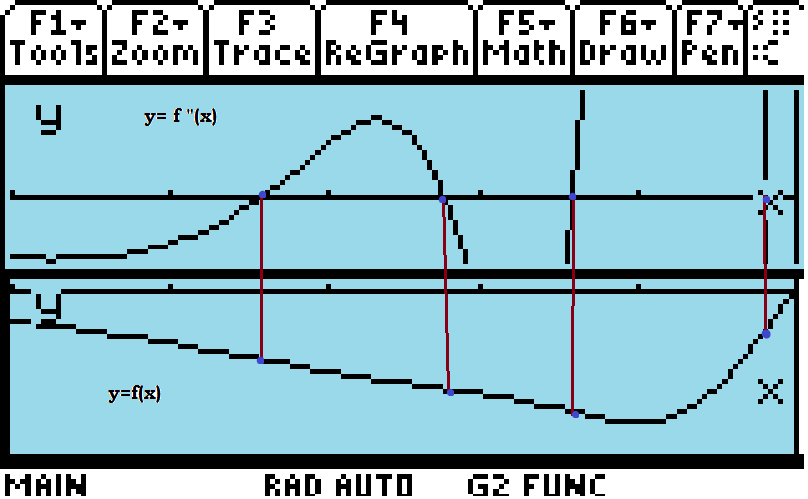
This second graph is a TOP-BOTTOM rendering in the TI89, with the upper graph representing f"(x) and the lower graph representing f(x).
Finally, you'll arrive at y = f"(x), where....
Verify this on your own!

