What are the quantum numbers for the 9th electron in flourine?
1 Answer
Explanation:
You know that fluorine has an atomic number equal to
Fluorine is located in period
Consequently, you can say that this electron will have a principal quantum number,
#n = 2#
Now, fluorine is located in group
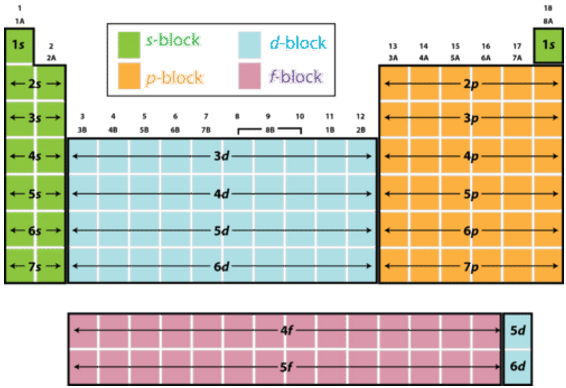
This implies that the angular momentum quantum number,
#l = 1#
This is the case because you have
#l =0 -># describes the#s# subshell#l = 1 -># describes the#p# subshell#l = 2 -># describes the#d# subshell
#vdots#
and so on. Next, for the
#m_l = {-1, 0, +1}#
By convention, you have
#m_l = -1 -># describes the#p_y# orbital#-># corresponds to groups#13# and#16# #m_l = color(white)(-)0 -># describes the#p_z# orbital corresponds to groups#14# and#17# #m_l = +1 -># descrbes the#p_x# orbital corresponds to groups#15# and#18#
Since the
#m_l = 0#
This electron will be added to the
Finally, the spin quantum number,
#m_s = {+1/2, - 1/2}#
Now, the
#m_s = -1/2#
because, by convention, electrons added to a half-filled orbital are assigned spin-down. The
You can thus say that the full quantum number set that describes the
#n = 2, l =1, m_l = 0, m_s = -1/2# The electron is located on the second energy level, in the
#2p# subshell, in the#2p_z# orbital, and has spin-down

