What are the quantum numbers of the five electrons of Boron?
1 Answer
Here's what I got.
Explanation:
Boron,
This means that a neutral boron atom will have a total of
Now, your tool of choice here will be boron's electron configuration, which looks like this
#"B: " 1s^2 2s^2 2p^1#
Since you have five electrons, you will need five sets of quantum numbers.
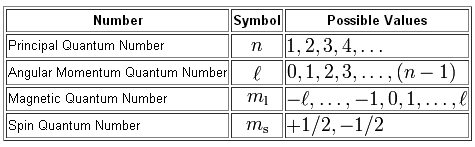
So, to make things interesting, let's start removing electrons one by one from the boron atom and describing them as we go.
The first electron will come from the orbital that's highest in energy. In this case, this electron will come from a 2p-orbital.
Now, the energy level is given by the principal quantum number,
Notice that
#l=0 -># the 2s-subshell#l=1 -># the 2p-subshell
The actual orbital in which the electron can be found is given by the magnetic quantum number,
For the p-subshell, you have a total number of three possible orbitals
#m_l = -1 -># the#p_x# orbital#m_l = 0 -># the#p_y# orbital#m_l = +1 -># the#p_z# orbital
Finally, the spin of the electron, which is given by the spin quantum number, can either by spin-up,
So, for the first electron, a valid set of quantum numbers will be
#n = 2, l=1, m_l = -1, m_s = +1/2#
Now for the second and third electrons, which will come from a 2s-orbital. This time, you will have
#n=2, l=0, m_l = 0, m_s = -1/2#
and
#n=2, l=0, m_l=0, m_s = +1/2#
Now you're down to the last two electrons, which reside on the first energy level, in the 1s-orbital
#n=1, l=0, m_l = 0, m_s = -1/2#
and
#n=1, l=0, m_l = 0, m_s = +1/2#

