What are the rules of transformation - specifically, of dilation, rotation, reflection and translation?
1 Answer
The rules for translation (shift), rotation, reflection and dilation (scaling) on a two-dimensional plane are below.
Explanation:
- Rules of translation (shift)
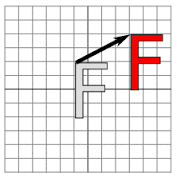
You need to choose two parameters: (a) direction of the translation (straight line with a chosen direction) and (b) length of the shift (scalar). These two parameters can be combined in one concept of a vector.
Once chosen, to construct an image of any point on a plane as a result of this transformation, we have to draw a line from this point parallel to a vector of translation and, in the same direction as chosen on the vector, move a point along this line by a chosen length.
- Rules of rotation
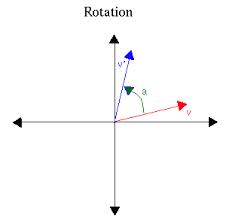
You need to choose two parameters: (a) center of rotation - a fixed point on a plane and (b) angle of rotation.
Once chosen, to construct an image of any point on a plane as a result of this transformation, we have to connect a center of rotation by a vector with our point and then rotate this vector around a center of rotation by an angle congruent to a chosen angle of rotation.
- Rules of reflection
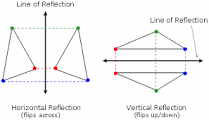
You need to choose only one parameter - the axis (or line) of reflection.
Once chosen, to construct an image of any point on a plane as a result of this transformation, we have to drop a perpendicular from our point onto an axis of reflection and extend it to the other side of the plane beyond this axis by the same distance.
- Rules of dilation ( scaling)
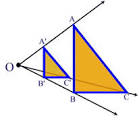
You need to choose two parameters - (a) center of scaling and (b) factor of scaling.
Once chosen, to construct an image of any point on a plane as a result of this transformation, we have to connect a center of scaling with our point and stretch or shrink this segment by a scaling factor, leaving the center of scaling in place. Factors greater than 1 will stretch the segment, factors from 0 to 1 are shrinking this segment. Negative factors reverse the direction of a segment to opposite side from the center.

