Question

What are three colligative properties of solutions?

Answer 1

1) The lowering of the solvent's vapor pressure.
2) The decrease in the solvent freezing point.
3) The increase in the solvent boiling point.

Heck, I could list a fourth:

4) The increase in osmotic pressure.

---

VAPOR PRESSURE REDUCTION

This follows from Raoult's Law for ideal solutions:

`P_A = chi_(A(v))P = chi_(A(l)) P_A^"*"`

where:

• `chi_(A(l))` is the mol fraction of the solvent `A` in the liquid phase.
• `chi_(A(v))` is the mol fraction of the solvent `A` in the vapor phase.
• `P_A` is the partial pressure of the solvent `A` above the solution.
• `P_A^"*"` is the partial pressure of the pure solvent `A` at the surface of the liquid phase.

Raoult's law relates the change in vapor pressure (the partial pressure above the liquid phase) to the mol fraction of the dissolved solute (`chi_(B(l))`) and the mol fraction of the vaporized solvent (`chi_(A(v))`).

Given that `chi_(A(l))` is always between `0` and `1`, it follows that `P_A <= P_A^"*"`. For a two-component solution, `chi_(A(l)) = 1 - chi_(B(l))`, where `B` is the other component (generally the solute).

Thus, for any quantity of solute added, the vapor pressure of the solvent above the solution decreases.

FREEZING POINT DEPRESSION AND BOILING POINT ELEVATION

The chemical potential `mu_A` for some solvent `A` in the solution as it relates to the mol fraction of `A` in an ideal solution is:

`mu_A = mu_A^"*" + RTlnchi_A`

where:

• `mu_A` is the chemical potential of the solvent in solution.
• `mu_A^"*"` is the chemical potential of the pure solvent.
• `chi_A` is the mol fraction of `A` in the solution. `chi_A = 1` if no solute is dissolved.

Chemical potential is just the molar Gibbs' free energy; it tends downwards, i.e. `Deltamu_A < 0` indicates a spontaneous process, or we say that `mu_A` runs downhill.

Given that any typical phase transition occurs at constant pressure, consider the following graph of `mu_A` vs. `T`:

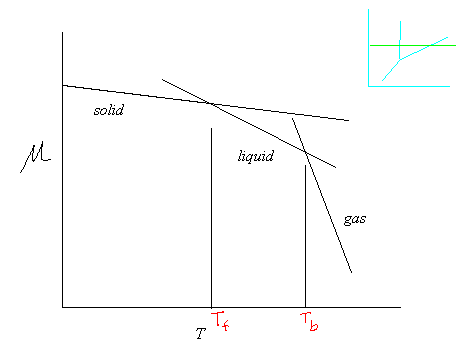
Now, note that in the above equation, we know that `chi_A <= 1`. It follows that `lnchi_A <= 0`, and that `mu_A < mu_A^"*"`. Therefore, `mu` for the solvent must decrease when solute is dissolved into the solvent.

When `mu` decreases for a liquid, the liquid line in the above diagram moves downwards, which shifts `T_f` leftwards and `T_b` rightwards.

This simultaneously explains why the solvent freezing point decreases when a solute is dissolved into a solvent, and why the solvent boiling point also increases (by less).

OSMOTIC PRESSURE ELEVATION

Imagine a U-shaped tube separated in the middle by a semi-permeable membrane.

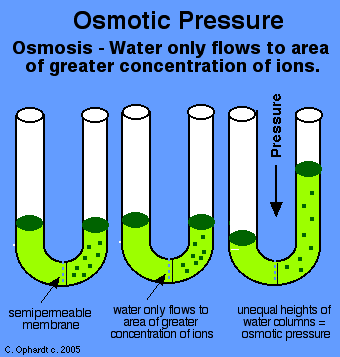
Osmotic pressure is the pressure that needs to be applied to prevent a pure solvent on one side from flowing to the other side due to a concentration gradient.

Osmotic pressure is given by:

`Pi = iMRT`

where `i` is the van't Hoff factor (the effective number of particles per dissolved solute particle), `M` is the molarity of the solution, and `R` and `T` are the universal gas constant and absolute temperature, respectively.

One can readily see that if `M uarr`, `Pi uarr` as well. Thus, higher concentration leads to higher osmotic pressure. The van't Hoff factor accentuates that, as it increases the effective concentration of the solute (`i >= 1`).

Conceptually, when a higher concentration of solute is on one side of the semi-permeable membrane, a higher concentration gradient exists with respect to the other side; the solvent wishes to flow into the side where the concentration is higher (the side with higher concentration "thirsts" for more solvent).

Therefore, higher concentration of solute increases the osmotic pressure, since one needs to apply a greater amount of pressure to prevent the solvent from flowing to the side with higher concentration.