What causes stellar parallax?
1 Answer
Let's first learn what is parallax, the reason for Stellar parallax.
Explanation:
We observe that when a nearby star is seen from earth, from two different observation points in time, against the background of a distant star or a cluster of stars; there is apparent movement of the star. We term this apparent movement of star as Stellar parallax.
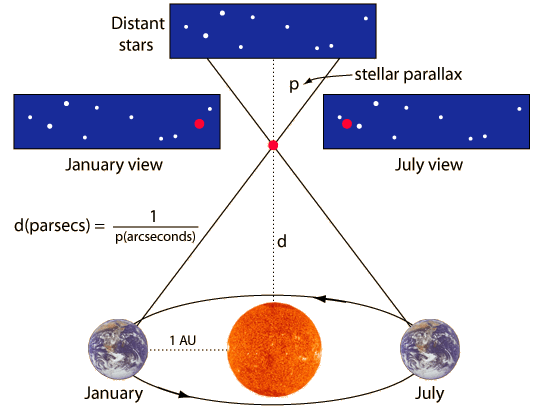
In the above picture we have an exaggerated view to understand Stellar parallax.
Red dot is a nearby star which is being viewed from earth against the background of group of distant stars.
Two observations are made, one in the month of January and the other in the month of July. Due to its rotation around Sun the earth is differently located for these observations.
We see that the view of group of distant stars remains same from both observation locations. Seen in blue strips.
However, due to the motion of earth, the nearby star appears shifted, even though the star itself has not moved. Position of the red dot in two blue strips in relation to group of distant stars. Also see the actual position of star under observation.
A right angled is formed by the distance
Application
The Stellar parallax is used to measure the distance to those stars which are close to the Sun and have measurable stellar parallax angle. For very distant stars the angle will be extremely small.
In the right triangle
Using small-angle approximations that if
where
This also gives the definition of parsec, (pc), the distance for 1 second of arc of stellar parallax.
