What could the fourth quantum number of a #2s^2# electron be?
1 Answer
Explanation:
As you know, a total of four quantum numbers are used to describe the positions and the spin of an electron in an atom.
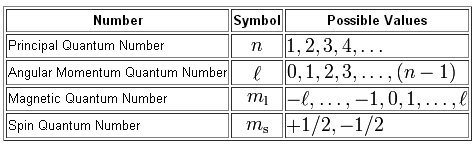
In your case, you must decide which possible values can be assigned to the fourth quantum number of an electron that resides in a
The principal quantum number describes the energy level, or shell, on which the electron resides. In this case, the electron is located on the second energy level, so
The angular momentum quantum number,
The magnetic quantum number,
#m_l = -l, -(l-1), ..., -1, 0, 1, ..., (l-1), l#
Finally, the spin quantum number,
Now, the s-orbital can hold a maximum of two electrons. The first electron will have
The first electron to occupy the 2s-orbital would be represented using the notation
This means that the fourth quantum number for a
#m_s = -1/2 -># spin-down
This implies that the 2s-orbital already contains an electron that has
#m_s = +1/2 -># spin-up
You can put all this together to find the quantum number set that describes the
#n=2, l=0, m_l = 0, m_s = -1/2#

