What does average rate of change mean?
1 Answer
The average rate of change of a function
Explanation:
Consider the following diagram:
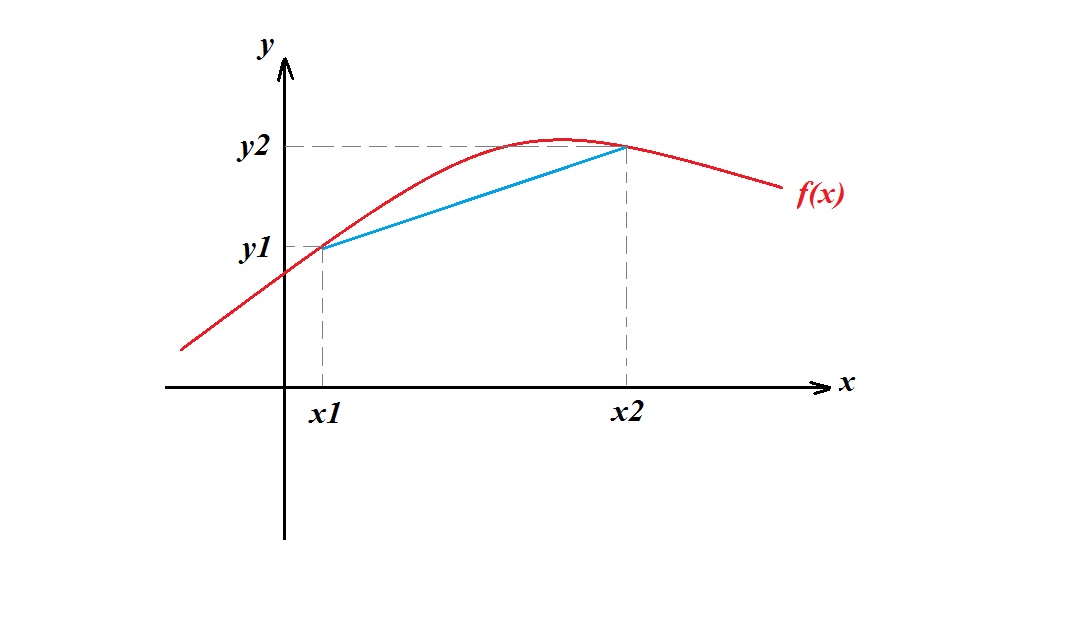
when
For example:
if
and:
you get that:
Average rate of change
This means that for your function:
Obviously your function is not a perfect straight line and it will change differently inside that interval but the average rate can only evaluate the change between the two given points not at each individual point.

