What does the equation #9y^2-4x^2=36# tell me about its hyperbola?
1 Answer
Before we start interpreting our hyperbola, we want to set it in standard form first. Meaning, we want it to be in
Once you have this, we can make a few observations:
- There is no h and k
- It is a
#y^2/a^2# hyperbola (which means that it has a vertical transverse axis.
Now we can begin to find some things. I will guide you through how to find some of the things most teachers will ask you to find on tests or quizzes:
- Center
- Vertices
3.Foci - Asymptotes
Look at the illustration below to get a good idea of what goes where and how the picture looks:
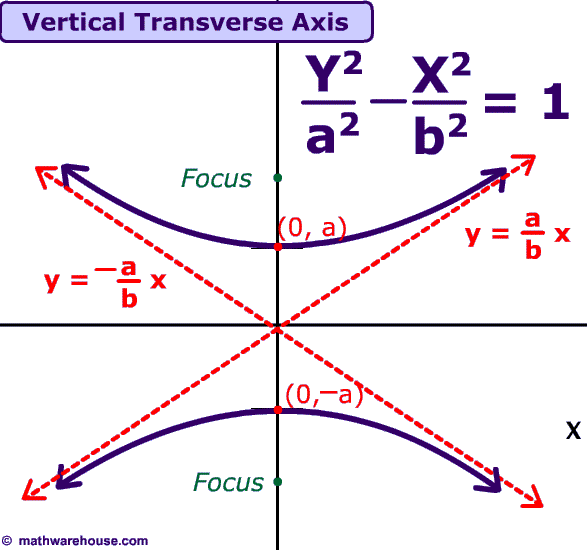
Since there is no h or k, we know that it is a hyperbola with a center at the origin (0,0).
The vertices are simply the points at which the hyperbola's branches begin to curve either way. As displayed in the diagram, we know that they are simply
So once we find
The foci are points that are the same distance from the vertices as the vertices are from the center. We usually label them with the variable
So now we plug in our
Our foci are always on the same vertical line as the vertices. So we know that our foci will be (0,
Lastly, we have our asymptotes. Asymptotes are simply "barriers" that prevent the branches from simply carrying straight on into space, and forcing them to curve.
As indicated by the picture, our asymptotes are simply the lines
So all we need to do is to plug in our stuff, and our asymptotes are
Hope that helps :)

