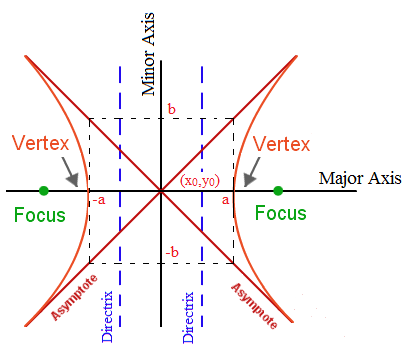
What does the equation #(x+2)^2/4-(y+1)^2/16=1# tell me about its hyperbola?
1 Answer
Jan 15, 2015
Quite a lot!
Here, we have the standard hyperbolic equation.
The center is at
The semi-transverse axis is
The semi-conjugate axis is
The vertices of the graph are
The foci of the graph are
The directrices of the graph are
Here is an image to help.