What does velocity mean in motions graphs?
1 Answer
Velocity is the change in position occurring over a change in time. Change in position is known as displacement, and is represented by
In position vs. time graphs, time is the independent variable and is on the x-axis, and position is the dependent variable and is on the y-axis. The velocity is the slope of the line, and is the change in position/change in time, as determined by
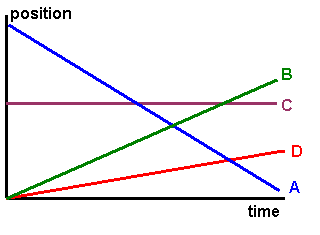
The following position vs. time graph shows the different possibilities when the velocity is constant. Constant velocity is represented by a straight line on a position vs. time graph.
On the graph, Line A represents constant negative velocity. Lines B and D represent constant positive velocity. The steeper slope of Line B indicates a faster velocity than D. Line C indicates a constant velocity of zero, meaning the object is at rest.
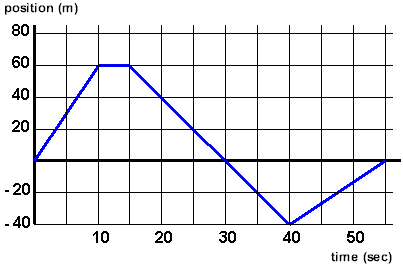
The position vs. time graph below indicates that the motion of an object is not constant. Suppose it is a car. For the first 10s, it travels at a constant positive velocity. For the next 5s, its velocity is zero, meaning it has stopped. For the next 25s it travels at a constant negative velocity, and for the last 15s, it travels at a constant positive velocity and returns to its initial position.