Begin by finding the slope via the formula: #m=(y_2-y_1)/(x_2-x_1)#
Let #(-8,11)->(color(blue)(x_1),color(red)(y_1))# and #(4,7/2)->(color(blue)(x_2),color(red)(y_2))# so,
#m=color(red)(7/2-11)/color(blue)(4-(-8))#
#m=color(red)(7/2-22/2)/color(blue)(4+8)larr# Find LCD for #7/2# and #11# and simplify
#m=color(red)(-15/2)/color(blue)(12)=-15/2*1/12larr# Apply the rule: #(a/b)/c=a/b*1/c# and multiply
#m=-15/24#
Now that we have found the slope, we can find the equation of the line using the point-slope formula: #y-y_1=m(x-x_1)#
Where #m# is the slope (which we just found) and #x_1# and #y_1# are the #x# and #y# values of either of the two given points. Substituting this information, we can easily find the equation of the line.
Recall that the slope, or #m#, Is #-15/24# and #x_1# and #y_1# are the #x# and #y# values of either of the two given points. I will choose to use the point #(-8,11)# as my #x_1# and #y_1# values just because I don't want to deal with the fraction. Just know that the point #(4,7/2)# will work just as well.
The equation of the line:
#y-(11)=-15/24(x-(-8))#
#y-11=-15/24(x+8)#
Note: We could leave the equation above as is and say that this is the equation of the line. We could also express the equation in #y=mx+b# form if desired in which case we must solve the equation for #y#
Solving for #y# would give us: #y=-5/8x+6#
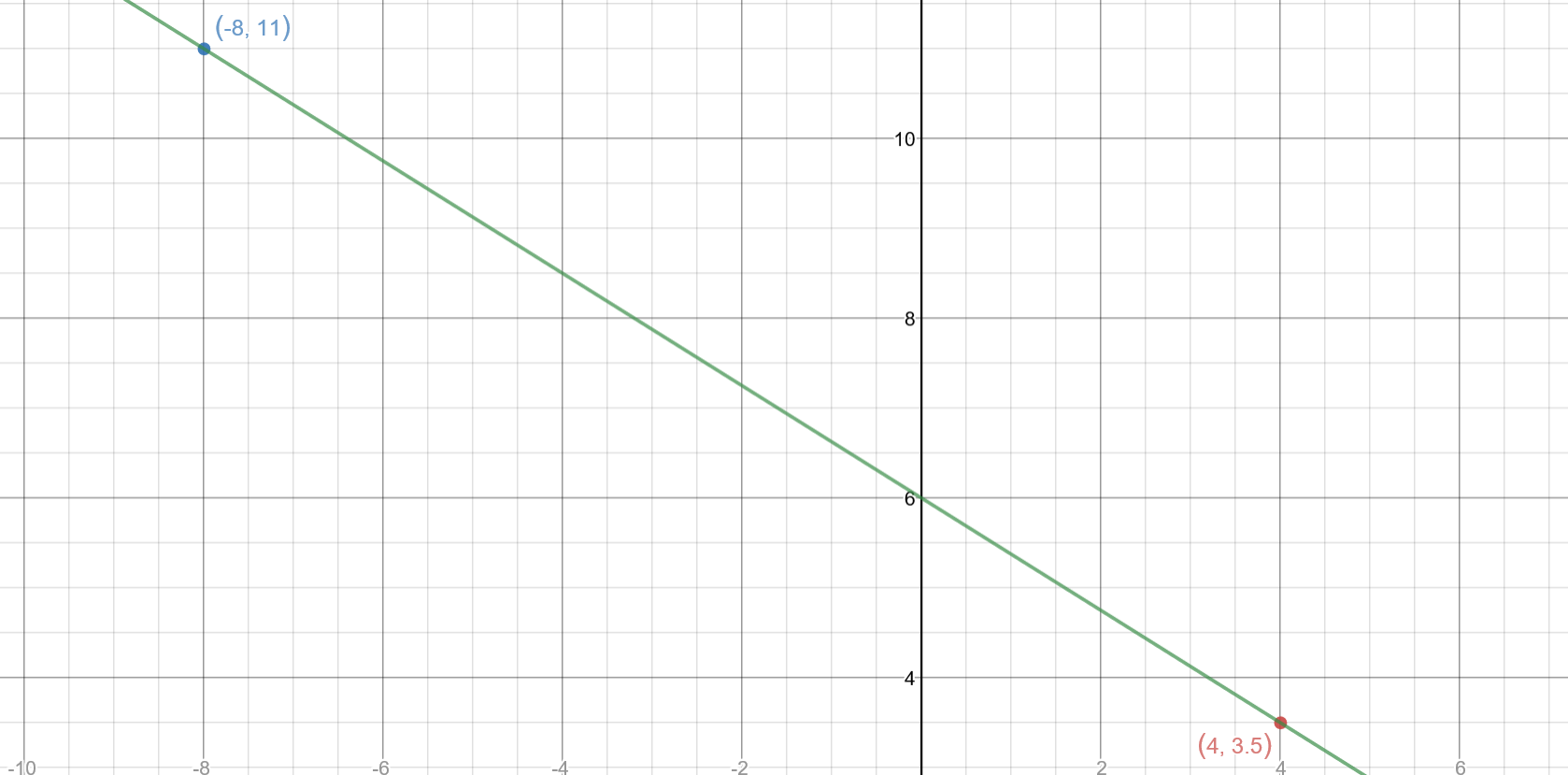
Below is what the line looks like along with the two points given in the problem.