What intervals is this function: #f(x)= x^5(lnx)# increasing and decreasing?
1 Answer
Dec 29, 2017
Explanation:
For
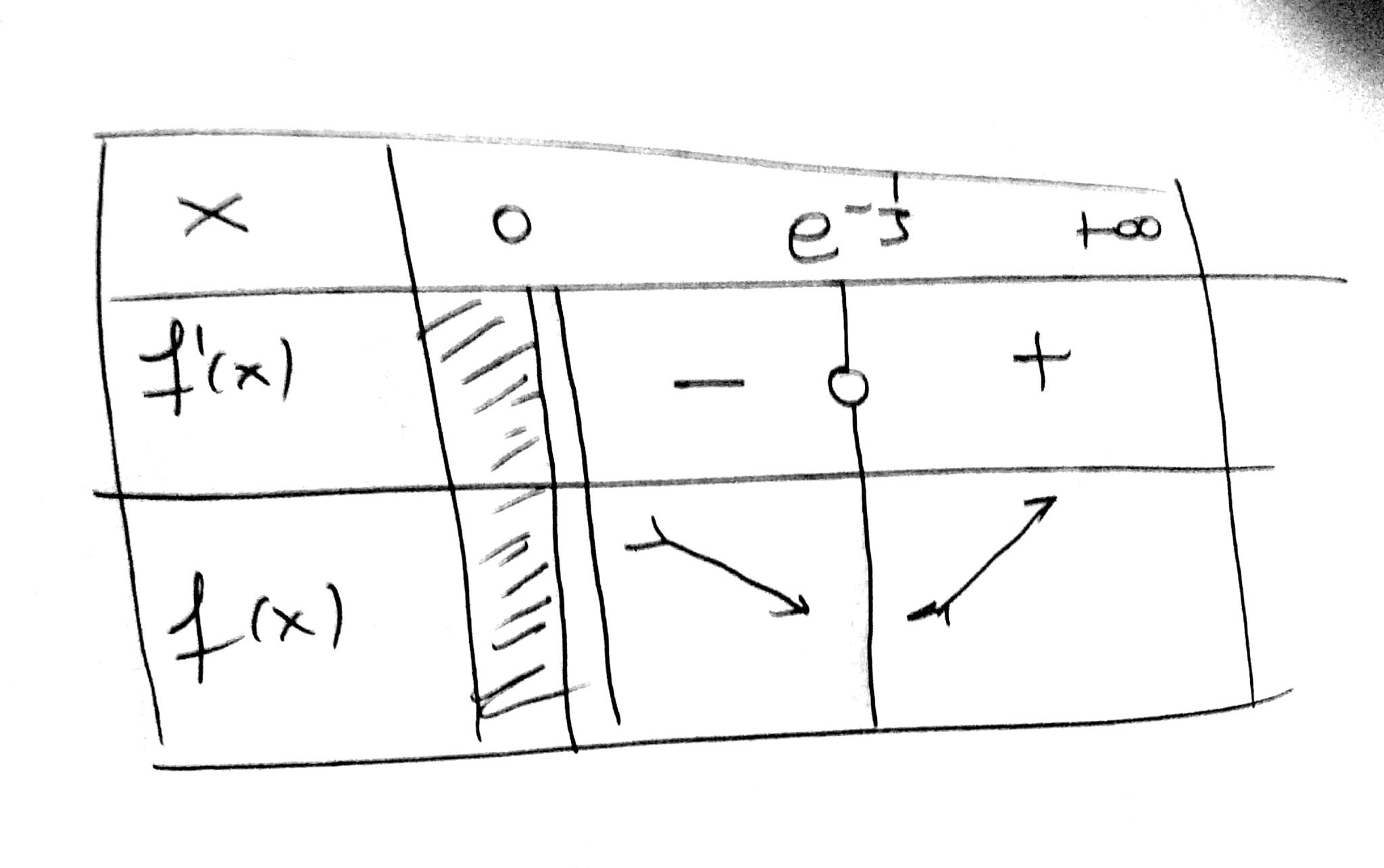
#f'(x)=0# #<=># #x^4=0# #<=># #x=0# -> Impossible because#x>0#
For
because
For
As a result we have,
-
#f# continuous in#(0,e^(-1/5)]# with#f'(x)<0# when#x# #in# #(0,e^(-1/5))# so#f# strictly decreasing in#(0,e^(-1/5)]# -
#f# continuous in#[e^(-1/5),+oo)# with#f'(x)>0# when#x# #in# #(e^(-1/5),+oo)# so#f# strictly increasing in#[e^(-1/5),+oo)#