Question

What is a combination of four quantum numbers that could be assigned to an electron occupying a 5p orbital?

Answer 1

Here's what I got.

Explanation:

As you know, you need four quantum numbers to describe the exact location of an electron in a atom and its spin.

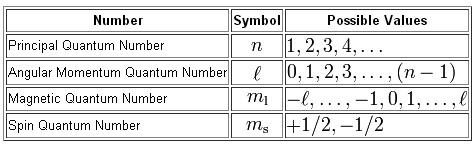
The principal quantum number, `n`, describes the energy level on which the electron resides. In your case, an electron that can occupy a 5p-orbital will have its principal quantum number equal to `5`

`n = 5 ->` the electron is located on the fifth energy level

The angular momentum quantum number, `l`, describes the subshell in which the energy can be found. For the fifth energy level, `l` can take values in the range

`l = 0, 1, 2, 3, 4`

Now, as its name suggests, a 5p-orbital will be located in a p-subshell, which is characterized by `l=1`.

`l = 1 ->` the electron is located in the 5p-subshell

The magnetic quantum number, `m_l`, tells you the exact orbital in which the electron can be found. A p-subshell can have three orbitals, regardless of energy level.

This means that you have three possibilities here, since the exact orbital is not specified by the problem

`m_l = {-1, 0, 1} ->` the electron can reside in any of the three 5p-orbitals

Finally, the spin quantum number, `m_s`, which describes the spin of the electron, can only have two possible values, `+1/2` for spin-up and `-1/2` for spin-down.

This means that an electron residing in a 5p-orbital can have

`m_s = {+1/2, -1/2} ->` either spin-up or spin-down

So, one set of quantum numbers that can describe an electron located in a 5p-orbital is

`n=5, l=1, m_l = -1, m_s = +1/2`

This electron is located on the fifth energy level, in the 5p-subshell, in the `5p_x` orbital, and has spin-up.

There are a total of six sets of quantum numbers that can be used here.