In the particle-in-a-box model, #hatH# operates on the wave function #psi_n#, which describes the state of a quantum mechanical system at quantized energy level #n#. The energy #E = K+0# you get back describes the energy state of a chemical system for still snapshots of the electron in an orbital at quantum level #n#.
This energy is the kinetic energy of the electron, determined by solving the equation #hatHpsi_n = (K+0)psi_n# where #K# is kinetic energy.
(No, you cannot divide by #psi_n#, you must operate on #psi_n# first and hope that you get it back afterwards)
It is often more succinctly said to be the Hamiltonian. It has many forms, but the easiest one to understand is the one in cartesian coordinates, written as:
#hatH = -(h^2)/(8pi^2m) [(del^2)/(delx^2) + (del^2)/(dely^2) + (del^2)/(delz^2)]#
That is the Hamiltonian Operator for three dimensions.
#h = 6.626xx10^(-34) J*s# and is Planck's constant
#m = 9.10938291xx10^(-31) kg# is the mass of the electron
#(del^2)/(delphi^2)#, where #phi = x,y,# or #z#, is the second-order partial derivative with respect to #x,y,# or #z#.
When #hatH# operates on the time-independent wave function #psi_n(x,y,z)#, which describes the state of a quantum mechanical system at quantized energy level #n#, we get back a value for the energy of the system when examining energy level #n#.
#hatHpsi_n = Epsi_n#
where:
#E = E_x + E_y + E_z#
To keep this simple, in the "1-dimensional" particle-in-a-box model, which describes, in the basic sense, an electron present in a 2D orbital of such a large size relative to the electron that there is essentially only one dimension (it is considered that the height of the 2D box is infinite), the only energy available to the electron is kinetic energy, and the potential energy (#V#) is zero.
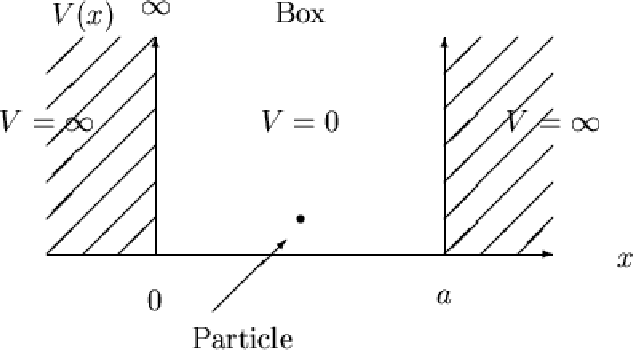
In the particle-in-a-box model, solving #hatHpsi_n# therefore gives the energy state of a chemical system for still snapshots of the electron in an orbital with quantum level #n#, where the electron has kinetic energy that is determined by solving the equation #hatHpsi_n = (K+0)psi_n# where #K# is kinetic energy. This kinetic energy is ideally identical every time you examine the same energy level, and so it is called the eigenvalue of the Hamiltonian.
It is possible to solve this exactly for Hydrogen, but it must be approximated by computers for anything with more than one electron.


