What is an equivalent fraction of 5/8?
1 Answer
Explanation:
Recall that an equivalent fraction is a fraction which is equal in value to another fraction, although its numerator and denominator may look different.
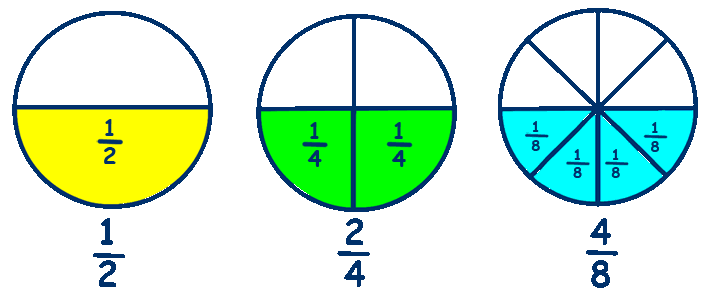
For example, in the following picture,
Although
#color(white)(XXXXXx)2/4color(white)(XXXXXXXXXx)4/8#
#color(white)(XXXX)=(2-:2)/(4-:2)color(white)(XXXXXX)=(4-:4)/(8-:4)#
#color(white)(XXXX)=1/2color(white)(XXXXXXxxx)=1/2#
Thus,
In your case, there are an infinite number of equivalent fractions to
For example:
#color(white)(Xx)5/8color(white)(XXXXXXX)color(purple)("or")color(white)(XXXXXXX)5/8#
#=(5color(red)(xx2))/(8color(red)(xx2))color(white)(XXXXXXXXXxxx)=(5color(red)(xx10))/(8color(red)(xx10))#
#=color(green)(|bar(ul(color(white)(a/a)10/16color(white)(a/a)|)))color(white)(XXXXXXXXXx)=color(green)(|bar(ul(color(white)(a/a)50/80color(white)(a/a)|)))#
However, keep in mind that you
For example, the following are
#10.6/16.6color(white)(iiii),color(white)(iiii)5.0/7.0color(white)(iiii),color(white)(iiii)152.73/614.46color(white)(iiii),color(white)(iiii)89.0/124.1#