Question

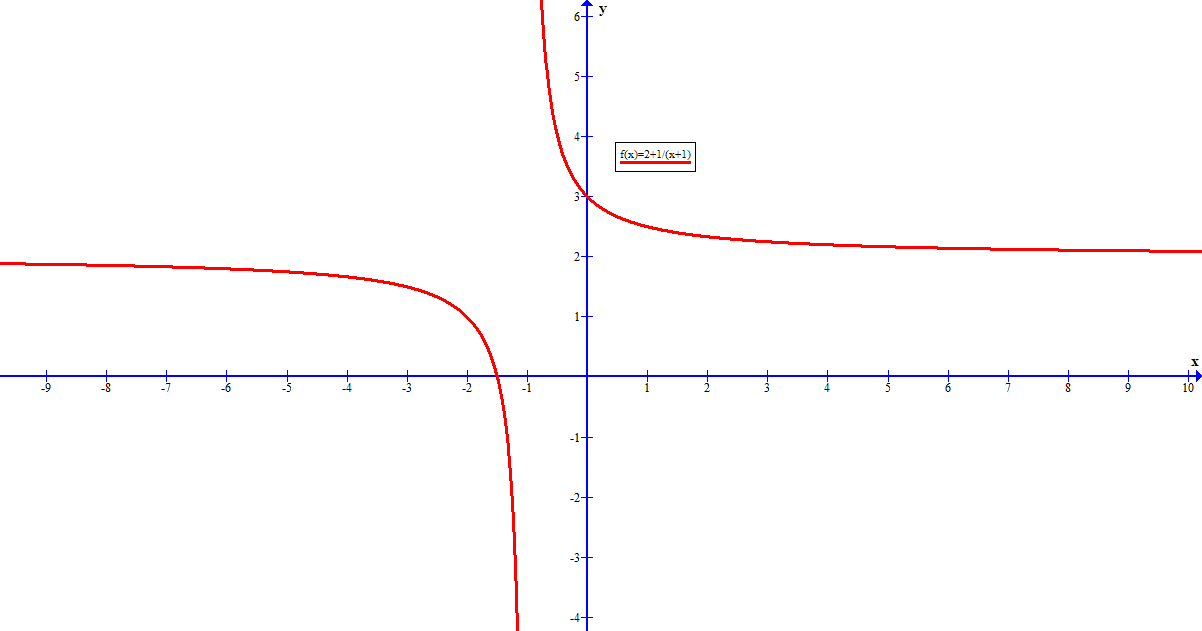
What is an example of a function that has a vertical asymptote at `x = -1` and a horizontal asymptote at `y = 2`?

Answer 1

`f(x) (=y) = 2+1/(x+1)`

Explanation:

We know that the relation `haty=1/hatx` has a vertical asymptote at `hatx=0` and a horizontal asymptote at `haty=0`

If we wish to shift all points left one unit (i.e. the vertical asymptote to `x=-1`) then we need to replace `hatx` with `x+1` (so when `x=-1` then `hatx=0`, the vertical asymptote).

Similarly to shift all points up two units (i.e. the horizontal asymptote to `y=2`) we need to replace `haty` with `y-2`

Therefore the required relation would become
`color(white)("XXX")y-2=1/(x+1)`

Converting this into function form (with `y=f(x)`)
we have
`color(white)("XXX")y=2+1/(x+1)`