The complex conjugate of an arbitrary complex number #z=a+bi# (with #a,b\in RR#) is #bar{z}=a-bi#.
Geometrically, in the complex plane, #bar{z}=a-bi# is a reflection of the point #z=a+bi# across the horizontal (real) axis.
Algebraically, it has the properties that the product #z*bar{z}# is real and, moreover, it equals the square of the modulus ("length") #|z|^2# of the complex number #z=a+bi#. Just do the algebra to see this:
#z*bar{z}=(a+bi)*(a-bi)=a^2-abi+abi-b^2*i^2=a^2+b^2# since #i^2=-1#. Also note that #a^2+b^2=(sqrt{a^2+b^2})^2=|z|^2#.
This is useful for dividing complex numbers. Given a division problem, written as a fraction, such as #(2+7i)/(3+8i)#, the trick to determining what this equals in the form #a+bi# is to multiply the top (numerator) and bottom (denominator) of this fraction by the complex conjugate of the bottom:
#(2+7i)/(3+8i)*(3-8i)/(3-8i)=(6-16i+21i-56i^2)/(9+64)=62/73+5/73 i#.
If you think about this trick for the abstract expression #1/z#, it implies that you can write it as #1/z=1/z*bar{z}/bar{z}=bar{z}/|z|^2=1/|z|*bar{z}/|z|#.
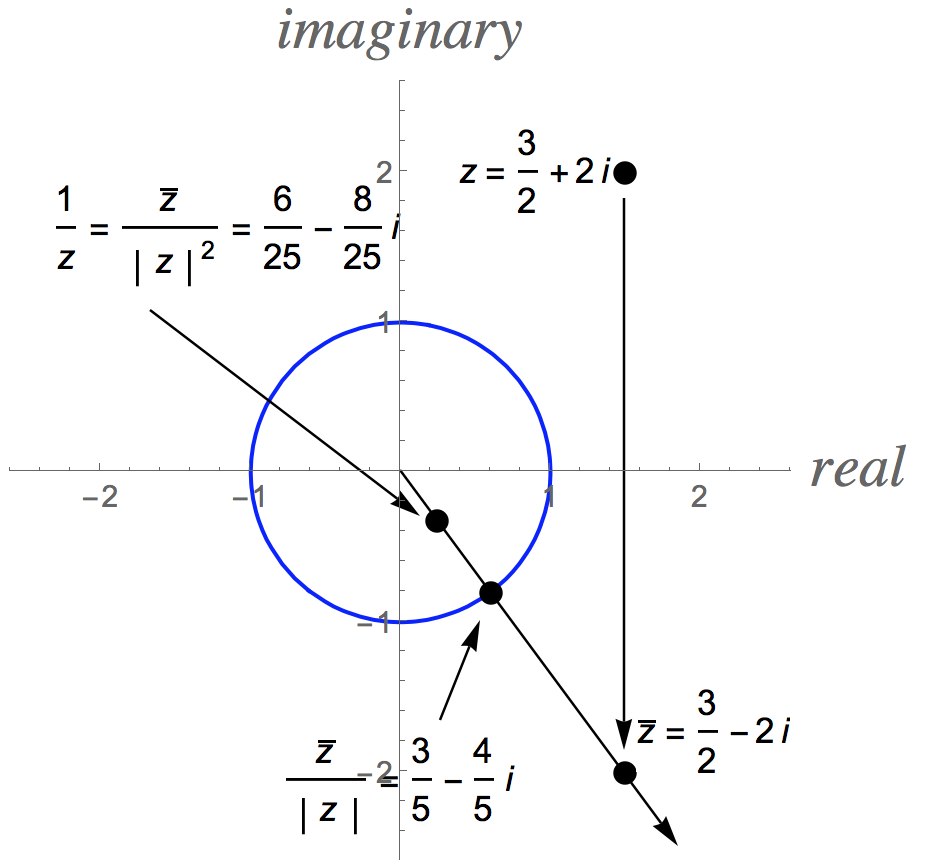
This has a nice geometric meaning. It implies that the "inversion mapping" (function) that sends #z# to its multiplicative inverse #1/z# (if #z!=0#) can be thought of geometrically as first reflecting #z# across the horizontal (real) axis to get #bar{z}#, then "normalizing" #bar{z}# to #bar{z}/|z|# to get a point 1 unit from the origin on the same ray from the origin through #bar{z}#. Finally, multiply this number by the scale factor #1/|z|# to get the number #1/z=1/|z|*bar{z}/|z|# on the same ray through the origin as #bar{z}#, but with a modulus of #1/|z|#.
Here's a picture to illustrate this process with #z=3/2+2i#, #bar{z}=3/2-2i#, #bar{z}/|z|=(3/2-2i)/sqrt{9/4+4}=(3/2-2i)/sqrt{25/4}=(3/2-2i)*2/5=3/5-4/5i#, and #1/z=bar{z}/|z|^2=(3/2-2i)/(25/4)=6/25-8/25 i#