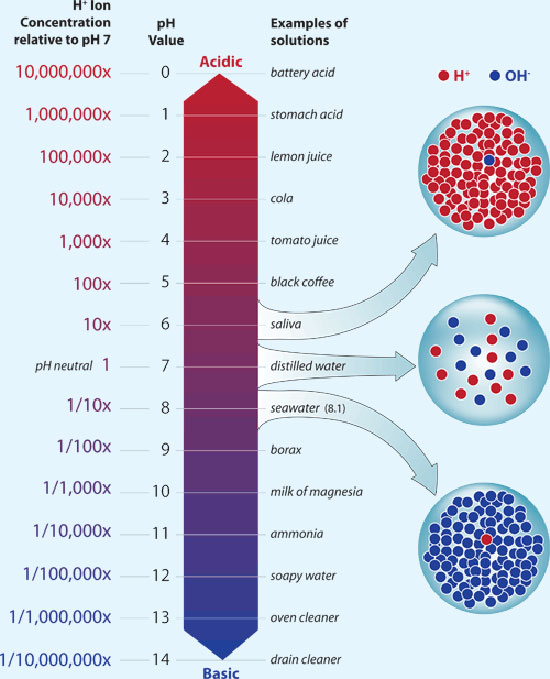
What is difference between a pH of 8 and a pH of 12 in terms of H+ concentration?
1 Answer
Here's what I got.
Explanation:
The pH of a solution is simply a measure of the concentration of hydrogen ions,
More specifically, the pH of the solution is calculated using the negative log base
#color(blue)(|bar(ul(color(white)(a/a)"pH" = - log(["H"_3"O"^(+)])color(white)(a/a)|)))#
Now, we use the negative log base
As you know, every increase in the value of a log function corresponds to one order of magnitude. For example, you have
#log(10) = 1#
#log(10 * 10) = log(10) + log(10) = 1 + 1 = 2#
#log(10 * 10^2) = log(10) + log(10^2) = 1 + 2 = 3#
and so on. In your case, the difference between a pH of
Keep in mind, however, that because you're dealing with numbers that are smaller than
More specifically, you have
#"pH"_1 = - log(["H"_3"O"^(+)]_1) = 8#
This is equivalent to
#["H"_3"O"^(+)]_1 = 10^(-"pH"_1) = 10^(-8)"M"#
Similarly, you have
#"pH"_2 = - log(["H"_3"O"^(+)]_2) = 12#
This is equivalent to
#["H"_3"O"^(+)]_2 = 10^(-"pH"_2) = 10^(-12)"M"#
As you can see, the first solution has a concentration of hydronium cations that is
#(10^(-8)color(red)(cancel(color(black)("M"))))/(10^(-12)color(red)(cancel(color(black)("M")))) = 10^color(red)(4)#
times higher than the concentration of hydronium cations of the second solution. This corresponds to the fact that you have
#"pH"_2 - "pH"_1 = 12 - 8 = color(red)(4)#
Simply put, a solution that has a pH that is