Question

What is interior angle of a polygon with 35 sides?

Answer 1

The interior angle of a 35-sided regular polygon is approximately `169.7`°, or `(33 pi)/35` in radians.

Explanation:

As an example, we have the following octagon:

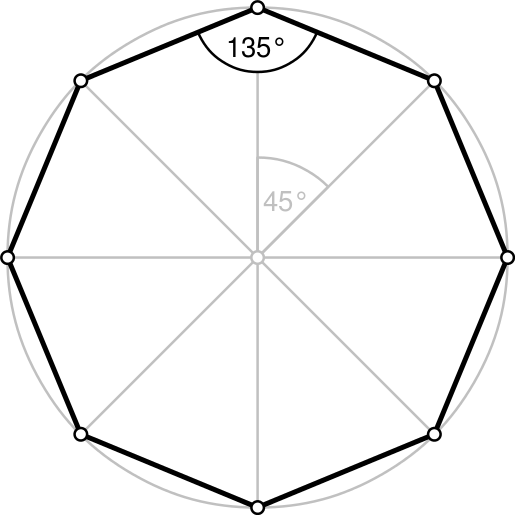
The interior angle of the octagon is 135°, which is the answer you're trying to find for a respective 35-sided polygon, but take note of the 45° angle at the center of the octagon.

A property that regular polygons share is that any such `n`-sided polygon can be divided into `n` isosceles triangles, as seen in the image.

We can use this to determine the angle touching the center of the polygon:

`(360°)/35~~10.29°`

Another important thing to notice in the image is that the interior angle is the sum of equal angles between two isosceles triangles.

As such, we do not need to learn the individual angles of the triangles, and we arrive at our answer.

`180°-10.29°~~169.7°`

The same method can be applied using radians, yielding the result shown above.