It's often used as a population model and it's a step up in complexity and accuracy from an exponential growth model. An exponential growth model assumes the relative growth #\frac{\frac{dP}{dt}}{P}# of a population is constant, which is unrealistic in the long run, whereas logistic growth assume the relative growth #\frac{\frac{dP}{dt}}{P}# can be thought of as a linearly decreasing function of #P#, say #\frac{\frac{dP}{dt}}{P}=k*(1-\frac{P}{L})#, so that #\frac{dP}{dt}=kP(1-\frac{P}{L})#. The constant #L# is called the carrying capacity of the environment.
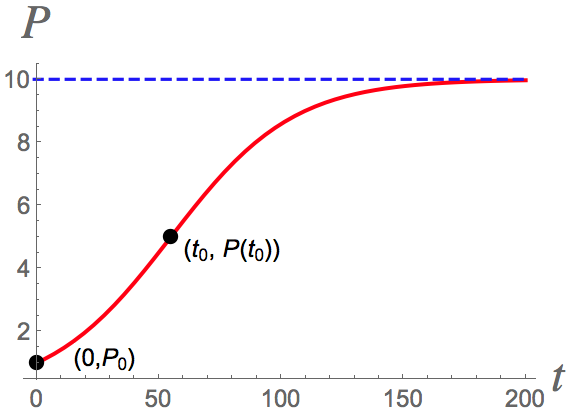
If you solve this differential equation using separation of variables and the initial condition #P(0)=P_{0}#, you'll get #P(t)=\frac{P_{0}Le^{kt}}{P_{0}e^{kt}+L-P_{0}}=\frac{L}{1+\frac{L-P_{0}}{P_{0}}e^{-kt}}#. This can also be written as #P(t)=\frac{L}{1+e^{-k(t-t_{0})}}#, where #\frac{L-P_{0}}{P_{0}}=e^{kt_{0}#. Note that #P(t_{0})=\frac{L}{2}#.
For #0 < P_{0} < L#, the graph of #P(t)# is an increasing function of #t# that looks somewhat like an elongated "S" (the technical name for the shape is "sigmoidal") with #\lim_{t\rightarrow\infty}P(t)=L#. It turns out that #t_{0}=\frac{1}{k}ln(\frac{L-P_{0}}{P_{0}})# is the time when the graph of #P(t)# has an inflection point (changing from concave up to concave down). See the figure below.