What is one method for proving the Pythagorean Theorem?
1 Answer
There are numerous ways but the most simple one is this
Explanation:
I really enjoyed this proof when I learnt it for the first Time .there is plenty of history behind it (;
So let me give you a timeline of the various mathematician's proof of this theorem
1)Bhaskara Method;(when I don't know)
He provided 2 proofs;
1st proof
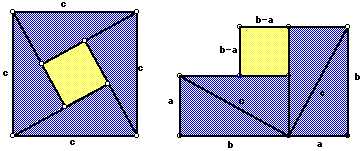
Consider the above figures;
In the above diagrams, the blue triangles are all congruent and the yellow squares are congruent. First we need to find the area of the big square two different ways. First let's find the area using the area formula for a square.
Area of the blue triangles
Area of the yellow square
Area of the big square
What??? We are there already we have arrived at the Pythagorean theorem
Now The second way involves similarity which I am not sure you are exposed to but if you want it ..Just comment (;)
Now Another method is the James Garfield method ;
I may suggest a video for the same but anyhow i will explain if you have any difficulties;

